Deep Learning

Sentencias básicas en Python

Francisco Plaza Vega

francisco.plaza.v@usach.cl

Ingeniería en Estadística

1 Instalación

Instalar python 3.X mediante el framework de ANACONDA
Para actualizar anaconda, se abre la línea de comandos (Anaconda prompt)
- conda update conda
- conda update --all
Además utilizar el comando conda para instalar los paquetes que utilizaremos durante esta parte del curso (se debe usar la línea de comandos):
- conda install numpy
- conda install scipy
- conda install matplotlib
- conda install pandas
- conda install scikit-learn
- conda install statsmodels

Para la programación podremos utilizar la IDE de Python llamada SPYDER o los notebooks de Jupyter, que vienen instalados con anaconda. También podremos utilizar Google Colab.
Si los paquetes ya se encuentran instalados, se utiliza el comando conda update nombre_paquete para actualizarlos.
La utilidad de los paquetes es la siguiente:
- Numpy: utilizado para manipulación matricial
- Scipy: posee herramientas estadísticas y de computación científica
- Matplotlib: utilizado para graficar
- Pandas: estructuras de datos para hacer estudios estadísticos
- Scikit-learn: Herramienta para machine learning y minería de datos
- Statsmodels: también posee herramientas estadísticas y de computación científica

2 Introducción

Algunos tutoriales gratuitos:

2.1 Operadores Aritméticos

Símbolo	Significado
`+`	Suma
`-`	Resta
`-`	Negativo
`*`	Multiplicación
`**`	Exponente
`/`	División
`//`	División entera
`%`	Módulo

Ejemplo:
Solicitar que el usuario ingrese dos números y entregar los resultados de los diferentes operadores.

#Leer números ingresados por el usuario
n1 = int(input("Ingrese un número: "))
n2 = int(input("Ingrese un número: "))
print("Suma = ", n1 + n2)
print("Resta = ", n1 - n2)
print("Multiplicación = ", n1 * n2)
print("División = ", n1 / n2)
print("Exponente = ", n1 ** n2)
print("División entera = ", n1 // n2)
print("Módulo = ", n1 % n2)

Ejemplo:
Dado dos números ingresados por el usuario escribir el resultado de la división con una parte entera y con la parte fraccional.

#leer números y almacenarlos
n1 = int(input("Ingrese un número 1: "))
n2 = int(input("Ingrese un número 2: "))
print(n1, "/", n2, "=", n1/n2 )
print("parte entera =", n1//n2)
print("parte decimal =", n1/n2 - n1//n2 )

2.2 Operadores relacionales

Símbolo	Significado
`==`	Igual que
`!=`	Distinto que
`<`	Menor que
`>`	Mayor que
`<=`	Menor o igual que
`>=`	Mayor o igual que

2.3 Operadores Lógicos y tabla de valores

Símbolo
`and`
`or`
`not`
`xor` (`^`)

	and		or		xor
	False	True	False	True	False	True
——-	——-	——-	——-	——-	——-	——-
True	False	True	True	True	True	False
False	False	False	False	True	True	False

not
False	True
True	False

Ejemplo:
Solicitar al usuario que ingrese valores lógicos aplicar los operadores lógicos.

#Leer números ingresados por el usuario
p = bool(int(input("Ingrese 0 (Falso) o 1 (Verdadero) :")))
q = bool(int(input("Ingrese 0 (Falso) o 1 (Verdadero) :")))
print("p =",p, " not p = ", not p)
print("q =",q, " not q = ", not q)
print(p," and ", q, " es ", p and q)
print(p," or ", q, " es ", p or q)
print(p," xor ", q, " es ", p ^ q)

Ejemplo:
Determinar el valor de verdad de (p and q) or (not p and q) para p y q, ingresados por el usuario.

p = bool(int(input("Ingrese 0 (Falso) o 1 (Verdadero) :")))
q = bool(int(input("Ingrese 0 (Falso) o 1 (Verdadero) :")))
print((p and q) or (not p and q))

2.4 Precedencia de los operadores

Prioridad	Operador	Descripción
1	**	Exponente
2	+ -	Símbolo unario positivo o negativo
3	* / % //	Multiplicación, división, módulo
4	+ -	Suma y resta
5	&	operador lógico bitwise and
6	\|^	operador lógico bitwise or, xor
7	<= < > >=	operadores de comparación
8	<> == ! =	operadores de igualdad.
9	= %= /= *=	operadores de asignación
9	//= -= += **=	operadores de asignación
10	is is not	operadores de identidad
11	in in not	operadores de membresía
12	not or and	operadores de lógicos

Ejemplo:
Cuál es el resultado de la siguiente operación:

\[3 * 5 / 2 - 4 ** 2 <= 5 - 3 / 2 ** 3\ and\ True\]

3 Manejo básico de objetos

En Python, todo es un objeto, y todo objeto tiene tres propiedades: identidad, tipo, y valor. La identidad es una dirección dada por Python que no cambia. El tipo puede ser cualquiera de los siguientes.

None: representa la ausencia de un valor.
Números: Python tiene tres tipos de números:
- Entero
- Punto flotante (puede almacenar números con decimales)
- Complejo (puede almacenar la parte real e imaginaria de un número
Secuencias: Son colecciones ordenadas de elementos. Hay tres tipos de secuencias en Python:
- Cadenas (strings)
- Tuplas (tuples)
- Listas (lists)

Las cadenas de caracteres son muy utilizadas en python. Por ejemplo, creemos una variable con algún nombre.

nombre = "Francisco"
nombre

Podemos concatenar varias cadenas de caracteres, y de varias formas, añadiendo otra variable que almacene el apellido de Francisco:

nombre = "Francisco"
apellido = "Plaza"
print(nombre+apellido)

FranciscoPlaza

print(nombre+" "+apellido)

Francisco Plaza

print(nombre, apellido)

Francisco Plaza

print(nombre+" "+apellido+" Vega")

Francisco Plaza Vega

print(nombre, apellido, "Vega")

Francisco Plaza Vega

3.1 Listas

Una lista en Python es una colección de objetos, y representa la secuencia más general provista por el lenguaje. Las listas son modificables. Esto último quiere decir que un objeto de una posición particular puede ser cambiado por otro.

Puede ser una colección de elementos similares (homogéneos):

[1,2,3]

[1, 2, 3]

Puede contener elementos diferentes, (heterogéneos):

[1,"abc",2.4]

[1, 'abc', 2.4]

Puede ser vacía:

[]

[]

Puede contener a otra lista:

[[[1,2,],[3,4],7],5,6]

[[[1, 2], [3, 4], 7], 5, 6]

3.2 Tuplas

Una tupla contiene elementos que pueden ser tratados individualmente o en grupo. Por ejemplo, (x, y), puede ser impresa usando la función print(). Los elementos de la tupla pueden asignados de la siguiente forma:

tup1=(2,3)
print(tup1)

(2, 3)

Los elementos de la tupla pueden ser asignados a objetos individuales:

(a,b) = tup1

También se puede hacer sin usar los paréntesis:

a,b = tup1

Se pueden usar los elementos de la tupla de manera individual

(a,b) = tup1
print("El primer elemento de la tupla es", a)

El primer elemento de la tupla es 2

print("El segundo elemento de la tupla es", b)

El segundo elemento de la tupla es 3

Un detalle importante es que las tuplas son inmutables, es decir, un elemento de la tupla no puede ser cambiado de valor una vez que ya está definido:

tup1=(1,2)
# Ahora quiero cambiar el 1 por un 3:
tup1[0] = 3

La operación + en las tuplas, sirve para concatenar dos o más tuplas

tup1=(1,2)
tup2=(3,4)
tup3=(5,6)
tup4=tup1+tup2+tup3
tup4

(1, 2, 3, 4, 5, 6)

3.3 Manipular listas y tuplas

La funcionalidad para extraer partes de alguna lista o tupla es análoga a lo visto en R, supongamos que tenemos una variable denominada numeros, entonces

numeros = [111, 222, 333, 444, 555, 666]
numeros[0:3]
numeros[:-2]

3.3.1 Métodos para añadir elementos a listas

Método append

lista1 = ['Marcos', 'Roberto', 'Celeste', 'Margarita']
print (lista1)

lista1.append ('Alex')
print (lista1)

Método insert

lista1 = ['Marcos', 'Roberto', 'Celeste', 'Margarita']
print (lista1)

lista1.insert (1, 'Alex')
print(lista1)

3.3.2 Métodos para eliminar elementos de listas

Método pop

lista1 = ['Marcos', 'Roberto', 'Celeste', 'Margarita']
print (lista1)

lista1.pop(1)
print(lista1)

Método remove

lista1 = ['Marcos', 'Roberto', 'Celeste', 'Margarita']
print (lista1)

lista1.remove('Marcos')
print(lista1)

3.4 Ejercicios

Escriba un programa para intercambiar dos números.
Pregunte al usuario las coordenadas de un punto en el plano y encuentre la distancia desde el origen $(0,0)$.
Pregunte al usuario por dos puntos (coordenadas) y encuentre la distancia entre ellas.
Pregunte al usuario por tres puntos y halle si son o no colineares.
Dada la pregunta 4., si los puntos no son colineares, entonces halle el tipo de triángulo que forman (equilátero, isósceles o escaleno).
En la pregunta anterior, determine si el triangulo es de ángulo recto.
En la pregunta número 4., encuentre los ángulos del triángulo.
Pregunte al usuario para ingresar dos puntos y encuentre si están a igual distancia que desde el origen.
En la pregunta número 8., encuentre le ángulo entre la línea que une los puntos y el origen.

4 Estructuras de Control

Una estructra de control es un bloque de código que permite agrupar instrucciones.

Se tienen dos tipos de estructuras de control:

Estructuras de control condicionales
Estructuras de control iterativas

En python, los bloques de código se identifican con la identación que consiste en añadir espacios en blanco:

Se puede usar la tecla de tabulación, o espacios, pero se debe ser consistente con el espaciado.
La identación indicará que las instrucciones forman parte de una misma estructura de control.

4.1 Estructuras de control condicionales

Las estructuras de control condicionales son aquellas que permiten evaluar evaluar si se cumple una condición y de esta forma decidir qué acción ejecutar

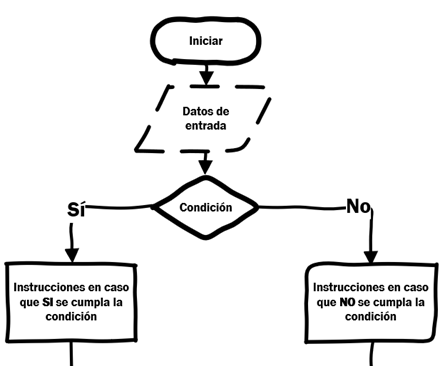
Estructuras de control condicionales

Ejemplo
EL costo de inscripción a un curso de verano es de $5000, sin embargo si la persona tiene carnet de estudiante, entonces se le aplica un descuento del 20%. Mostrar el monto total a pagar.

costo_curso = 5000
c = input("Tiene Ud. Carnet de estudiante? (S/N)")
if c == 'S':
    descuento = 5000*0.2
    costo_curso = 5000 - descuento
print("El costo del curso es:", costo_curso)

Ejemplo
A través del análisis de la discriminante $\Delta = b^2 - 4ac$ determinar si la ecuación cuadrática

\[ ax^2 + bx + c = 0 \]

tiene 2 soluciones reales ($\Delta>0$), 1 solución real ($\Delta=0$) o 2 soluciones imaginarias ($\Delta<0$). El usuario ingresa los valores para las variables a, b y c.

A = float(input("Ingrese a:"))
B = float(input("Ingrese b:"))
C = float(input("Ingrese c:"))
D = B**2 - 4*A*C
if D == 0:
    print(D)
    print("1 solución")
if D < 0:
    print(D)
    print("no tiene solución en R")
if D > 0:
    print(D)
    print("2 soluciones en R")

Condición IF y ELSE: ¿Qué pasaría si que queremos que se ejecute otra instrucción en caso que no se cumpla la condición?. En este caso debemos utilizar la sentencia ELSE de la siguiente manera:

Primeramente, declaramos nuestra condición IF como se detalló en la sección anterior
Seguidamente escribimos “else” más dos puntos
Detallamos las instrucciones que deseamos ejecutar, recordar presionar tabulación antes.

Condición ELIF: Si deseamos ejecutar más de una condición debemos ejecutar la sentencia ELIF. Es una contracción de ELSE IF la cual se ejecuta en el siguiente orden:

Primeramente, se evalúa la condición IF.
Si la condición de IF es cierta se ejecutará su instrucción y para la condición.
Pero en caso que la condición IF no se cumpla se evaluará la condición ELIF.
En caso que las condiciones de IF y ELIF no se cumplan se ejecutará las instrucciones de ELSE.

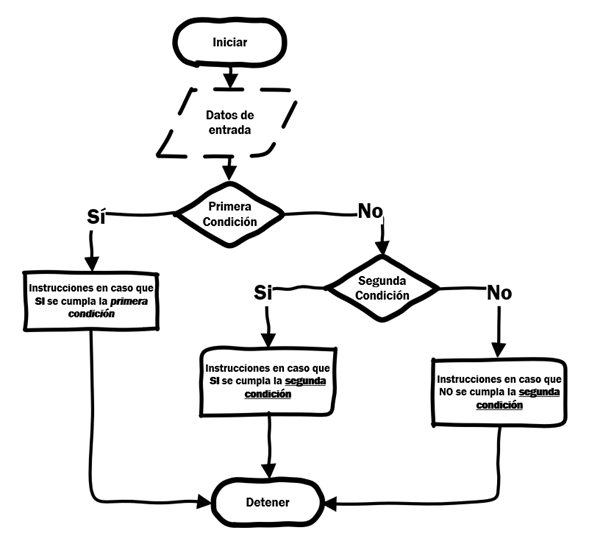
Estructuras de control condicionales más complejas

Ejemplo:
Dada la nota final del estudiante indicar si el estudiante aprobó la asignatura con nota superior o igual a 4.0 o reprobó la asignatura con nota inferior a 4.0.

nota_final = float(input("Ingrese Nota Final:"))
if nota_final >= 4.0:
    print("Es estudiante aprobó la asignatura")
else:
    print("Es estudiante reprobó la asignatura")

Ejemplo:
Si queremos hacer un código que nos permita el ingreso dependiendo de la edad podríamos hacerlo así:

edad = 70
if (edad >= 65):
  print("Es adulto mayor, puede ingresar")
elif (edad >= 18):
  print("Es joven, puede ingresar")
else:
  print("Es menor de edad, no puede ingresar")

Es adulto mayor, puede ingresar

print("Fin del código")

Fin del código

4.2 Ciclos iterativos (for y while)

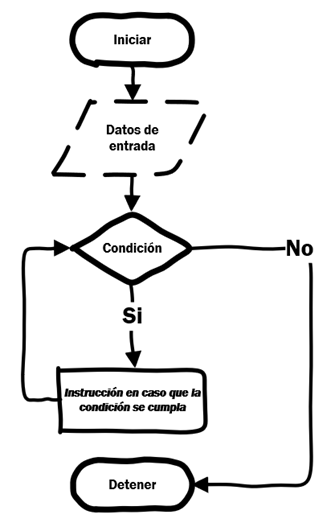
Estructuras de ciclos iterativos

Ciclos FOR:
Permiten ejecutar un número determinado de iteraciones, definidas a priori.

Para usar el ciclo FOR:

Escribimos “for”.
Definimos una variable donde se guardara el valor a iterar en cada ciclo.
Definimos el elemento a iterar que debe tener una longitud finita como un rango o lista.
Cerramos con dos puntos.

#Usamos range(inicio, fin, salto), para ir del 5 al 0, reduciendo en 1
for i in range(5, 0, -1):
  print(i)

Ciclos WHILE:
El ciclo WHILE ejecuta un fragmento de código mientras una condición preestablecida se cumpla.

Para ejecutar un ciclo WHILE se debe:

Escribir “while” primeramente
Seguidamente se escribe la condición a evaluar
Se cierra la sentencia con dos puntos

contador = 5
while (contador >=0):
  print(contador)
  contador-=1 #también se puede escribir contador = contador -1

4.3 Ejercicios Condicionales

Pedir un numero y mostrar si es par o impar.
Solicitar dos números y mostrar cual es el número mayor y menor.
Pedir un usuario y un password, verificar si estos son admin y 12345 respectivamente, si esto ocurre mostrar un mensaje de Bienvenido en caso contrario Acceso denegado.
Pedir en ingreso de tres calificaciones y mostrar un mensaje de APROBADO si su promedio es mayor a 50 y REPROBADO en caso contrario.
Ingresar un numero de día de semana del uno al siete y mostrar si es lunes, martes, miércoles, etc.
En una fábrica de computadoras se planea ofrecer a los clientes un descuento que dependerá del número de computadoras que compre. Si las computadoras son menos de cinco se les dará un 10% de descuento sobre el total; si el número de computadoras es mayor o igual a 5 pero menos de diez se otorga un 20%; si son 10 o mayor se dará un 40% de descuento. El precio de cada computadora es de 500$. Solicitar el número de computadoras compradas y mostrar el porcentaje de descuento y total.

4.4 Ejercicios Ciclos iterativos

Pedir un numero e imprimir todos los números pares entre 0 y el numero ingresado
Pedir un numero y mostrar su factorial.
Leer números enteros de teclado, hasta que el usuario ingrese el 0. Finalmente, mostrar la sumatoria de todos los números positivos ingresados.
Escriba un programa que pida números enteros mientras sean cada vez más grandes si introduce uno menor terminar el programa y mostrar la suma de todos.
Escribir un programa que solicite el ingreso de una cantidad indeterminada de números mayores que 1, finalizando cuando se reciba un cero. Imprimir la cantidad de números impares ingresados.
Crear un programa que permita al usuario ingresar los montos de las compras de un cliente (se desconoce la cantidad de datos que cargará, la cual puede cambiar en cada ejecución), cortando el ingreso de datos cuando el usuario ingrese el monto 0. Si ingresa un monto negativo, no se debe procesar y se debe pedir que ingrese un nuevo monto. Al finalizar, informar el total a pagar teniendo que cuenta que, si las ventas superan el total de $1000, se le debe aplicar un 10% de descuento.

5 Funciones

Si se necesita efectuar una tarea de programación que considera mayor complejidad, el poder dividir esa tarea en otras más pequeñas y más simples, ayudará a que el código sea más sencillo de escribir.

Las funciones tienen argumentos, los cuales denotan o que se ingresa a la función; es decir, el input de la función.
El valor de retorno de una función puede o no existir de manera explícita. Si el valor es explícito, éste será el resultado en la función. De lo contrario, un objeto vacío será el output de la función

5.1 Sintáxis

La sintáxis básica para crear una función es la siguiente:

def <nombre de la función>(<lista de parámetros>):
    <cuerpo de la función>
    return <el "output" de la función>

Nota: Cuidado con la identación!

5.2 Ejemplos

Ejemplo:
Programe una función que mutiplica dos números pasados como argumentos

def producto(num1,num2):
    prod=num1*num2
    print("el producto de", num1, "*", num2,"es", prod)
    producto(2,4)

Ejemplo, un poco más difícil:
Dada una lista, es posible crear una función que busque un elemento en una lista. Por ejemplo, si se ingresa la lista [1,2,3,4,5,6] y el valor 4, la función debería mostrar la posición 3 (recordando que las posiciones son contadas desde el 0). Encuentre el error del código que se presenta a continuación para que muestre la posición de lo encontrado, a partir del 0.

def buscar(L,item):
    bandera=0
    for i in L:
      if i==item:
        bandera=1
        print("posición", i)
    if bandera ==0:
      print("no encontrado")
L=[1,2,5,9,10]
buscar(L,5)

posición 5

5.3 Ejercicios

Escriba una función que calcule la media de $n$ números ingresados por el usuario.
Escriba una función que calcule la moda de $n$ números ingresados por el usuario.
Escriba una función que calcule la mediana de $n$ números ingresados por el usuario.
Escriba una función que calcule la desviación estándar de $n$ números ingresados por el usuario.
Escriba una función que encuentre el máximo de una lista de números ingresada por el usuario.
Escriba una función que encuentre el mínimo de una lista de números ingresada por el usuario.

6 Gráficos en Python: `matplotlib`

Como lo sugiere su nombre (en inglés), matplotlib es una librería de gráficos de python. Es útil para mostrar resultados, para estudiar el comportamiento de funciones, etc.

6.1 Gráfico de líneas

Usando la función plot(), se puede crear un gráfico de línea. Se puede definir la cuadrícula, el eje $x$ e $y$, sus etiquetas, escala, título, y opciones de visualización.

import matplotlib.pyplot as plt
import numpy as np
t = np.arange(0.0, 2.0, 0.01)
s = np.sin(2.5*np.pi*t)
plt.plot(t, s)
plt.xlabel('tiempo (s)'); plt.ylabel('voltaje (mV)'); plt.title('Onda seno')
plt.grid(True)
plt.show()

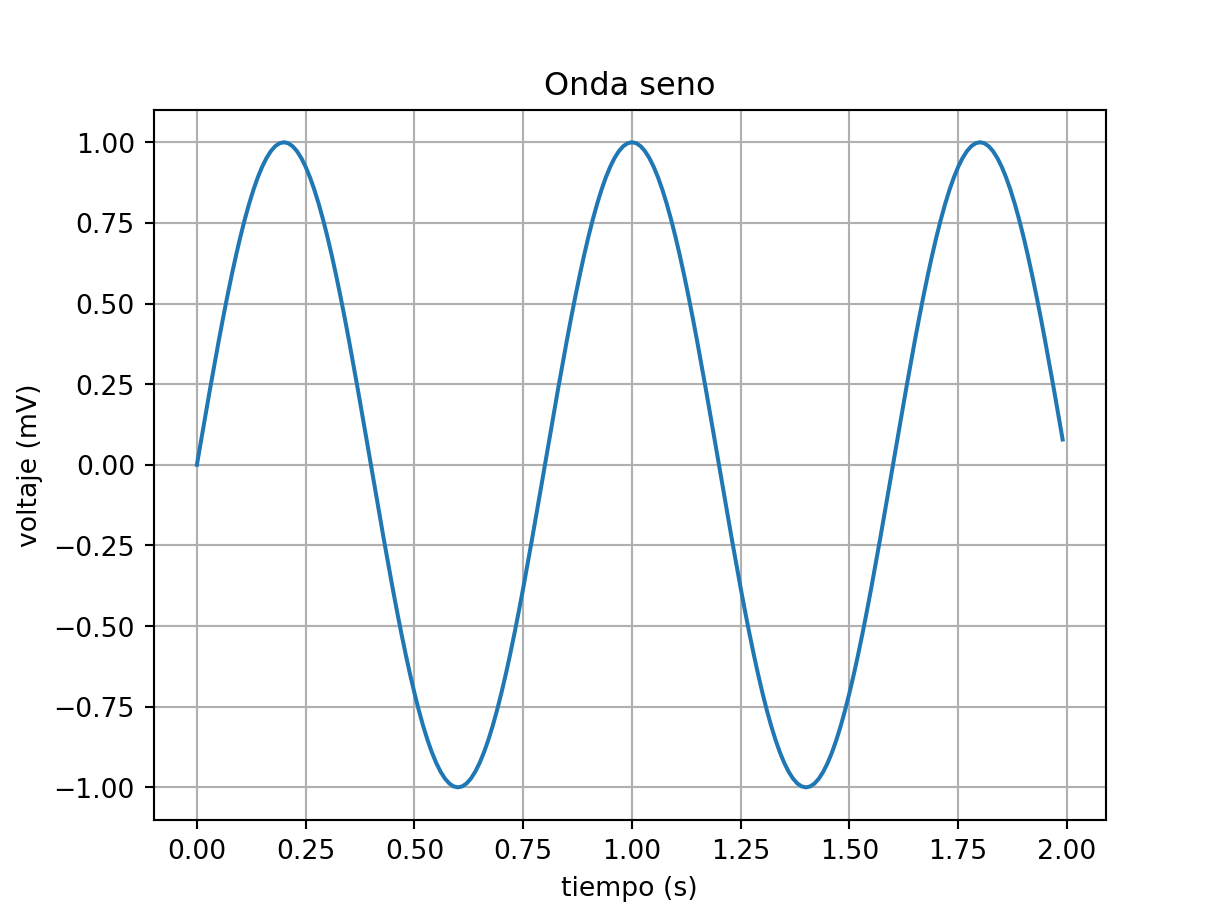
Graficando un arreglo (lista)

import matplotlib.pyplot as plt
import numpy as np
t = np.arange(0.0, 20.0, 1)
s = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
plt.plot(t, s)
plt.xlabel('Item (s)'); plt.ylabel('Valor') 
plt.title('Gráfico de líneas de Python: Graficando números')
plt.grid(True)
plt.show()

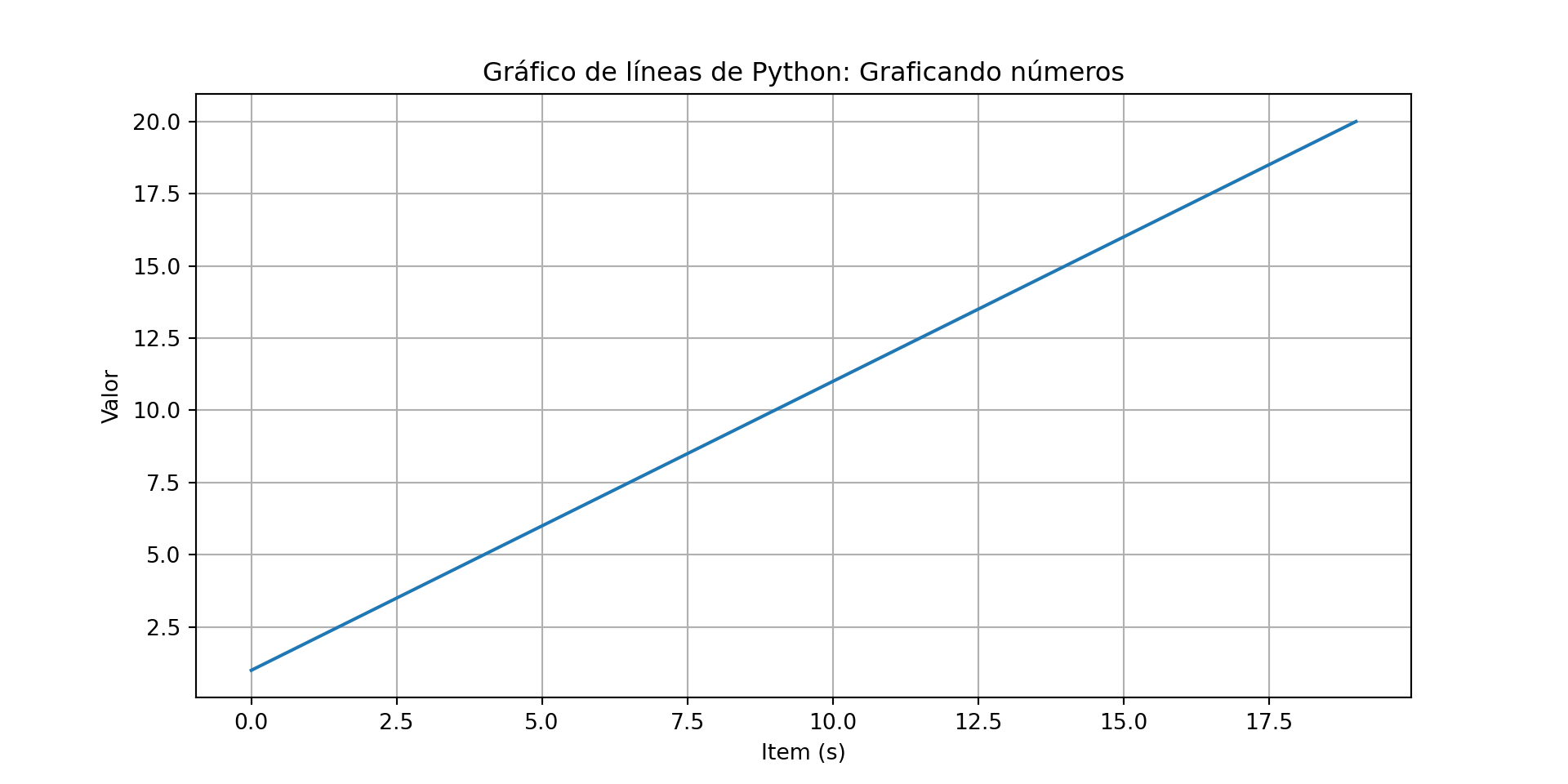
6.2 Gráficos múltiples

Si se quiere graficar múltiples líneas en un mismo gráfico, simplemente se llama a la función plot() múltiples veces.

import matplotlib.pyplot as plt
import numpy as np
t = np.arange(0.0, 20.0, 1)
s = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
s2 = [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]
plt.plot(t, s); plt.plot(t, s2);
plt.xlabel('Item (s)'); plt.ylabel('Valor')
plt.title('Gráfico de líneas de Python: Graficando números')
plt.grid(True)
plt.show()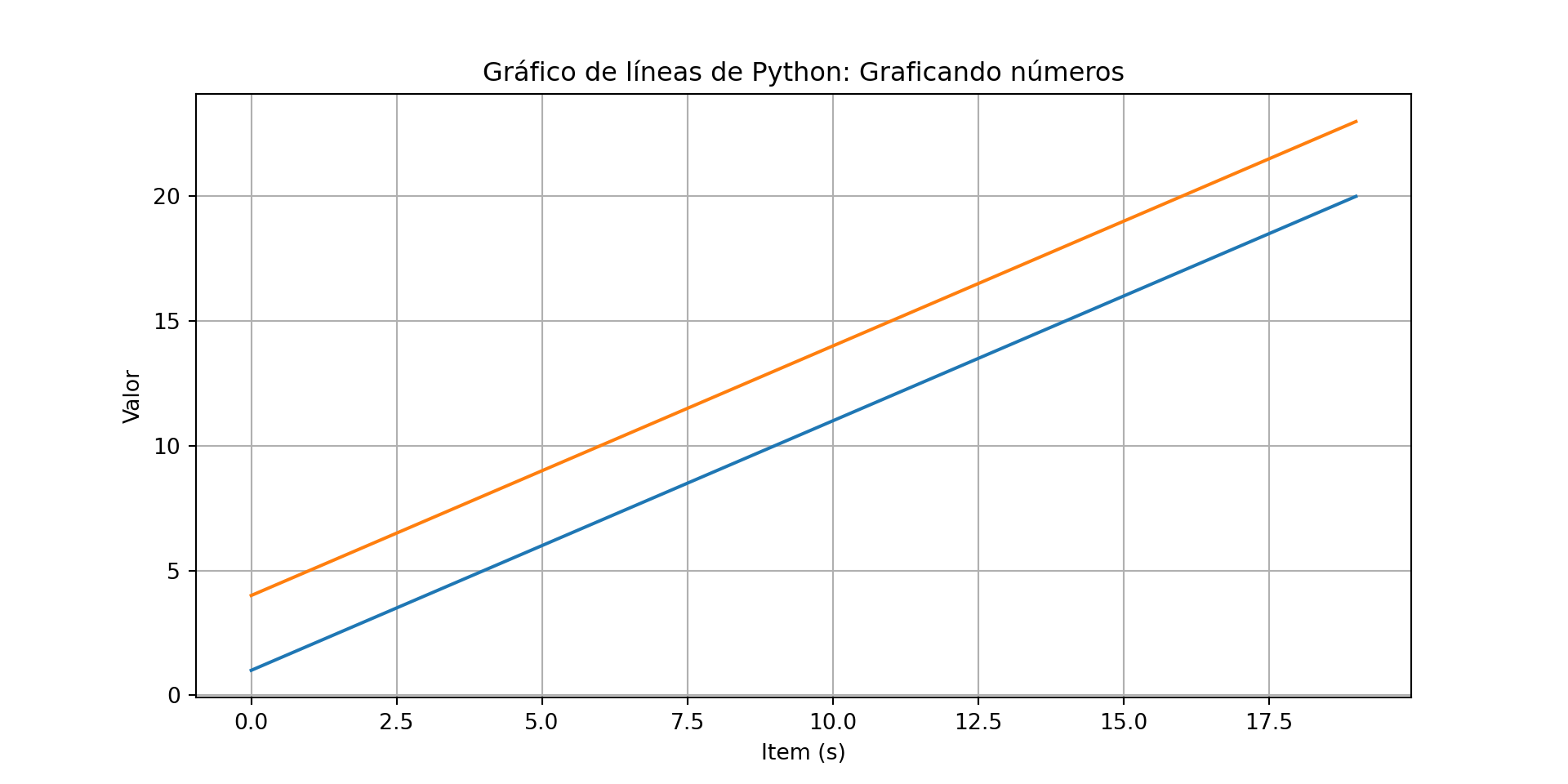

La función subplot() puede ser llamada para graficar dos o más gráficos en una figura. La librería soporta todo tipo de sub-gráficos, incluyendo horizontales ($n \times 1$), verticales ($1 \times n$) o cuadriculados de ($n \times m$).

#Ejemplo para una cuadrícula de 2 x 1
import matplotlib.pyplot as plt
from pylab import *
t = arange(0.0, 20.0, 1)
s = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
s2 = [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]
plt.subplot(2, 1, 1)
plt.plot(t, s)
plt.ylabel('Valor'); plt.title('Primer gráfico')
plt.grid(True)
plt.subplot(2, 1, 2)
plt.plot(t, s2)
plt.xlabel('Item (s)'); plt.ylabel('Valor'); plt.title('Segundo gráfico')
plt.grid(True)
plt.show()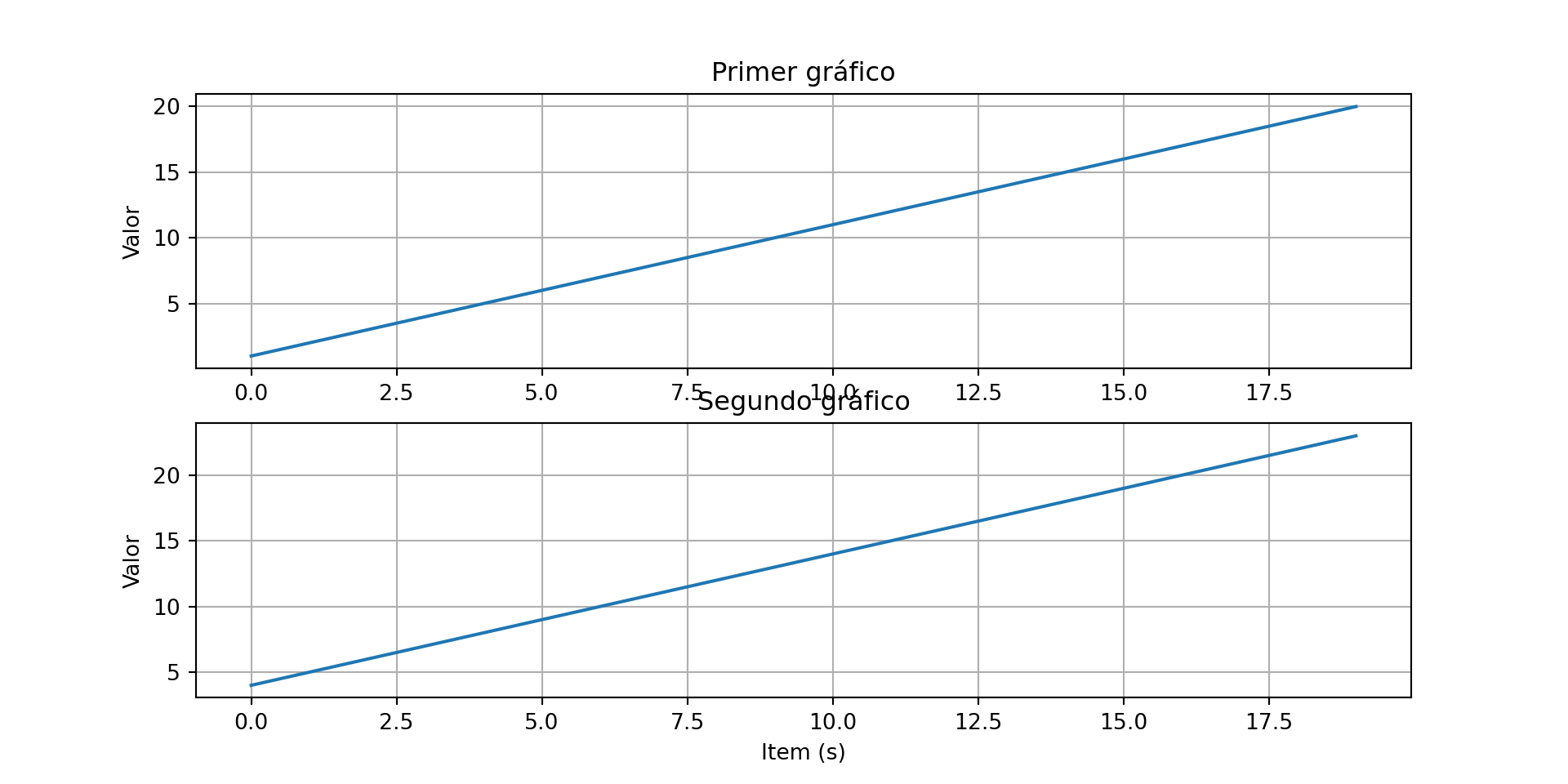

6.3 Gráficos de dispersión

Matplotlib tiene una función para crear gráficos de dispersión, o en inglés, scatterplots, llamada scatter(). Un gráfico de dispersión es un tipo de gráfico que muestra los datos como colección de puntos en el espacio. La posición de un punto depende de su valor 2-dimensional. donde cada valor es una posición en el eje horizontal y vertical.

import numpy as np
import matplotlib.pyplot as plt
# Crear los datos
N = 500
x = np.random.rand(N)
y = np.random.rand(N)
colors = (0,0,0)
area = np.pi*3
# Graficar
plt.scatter(x, y, s=area, c=[colors], alpha=0.5)
plt.title('Scatter plot'); plt.xlabel('x'); plt.ylabel('y')
plt.show()

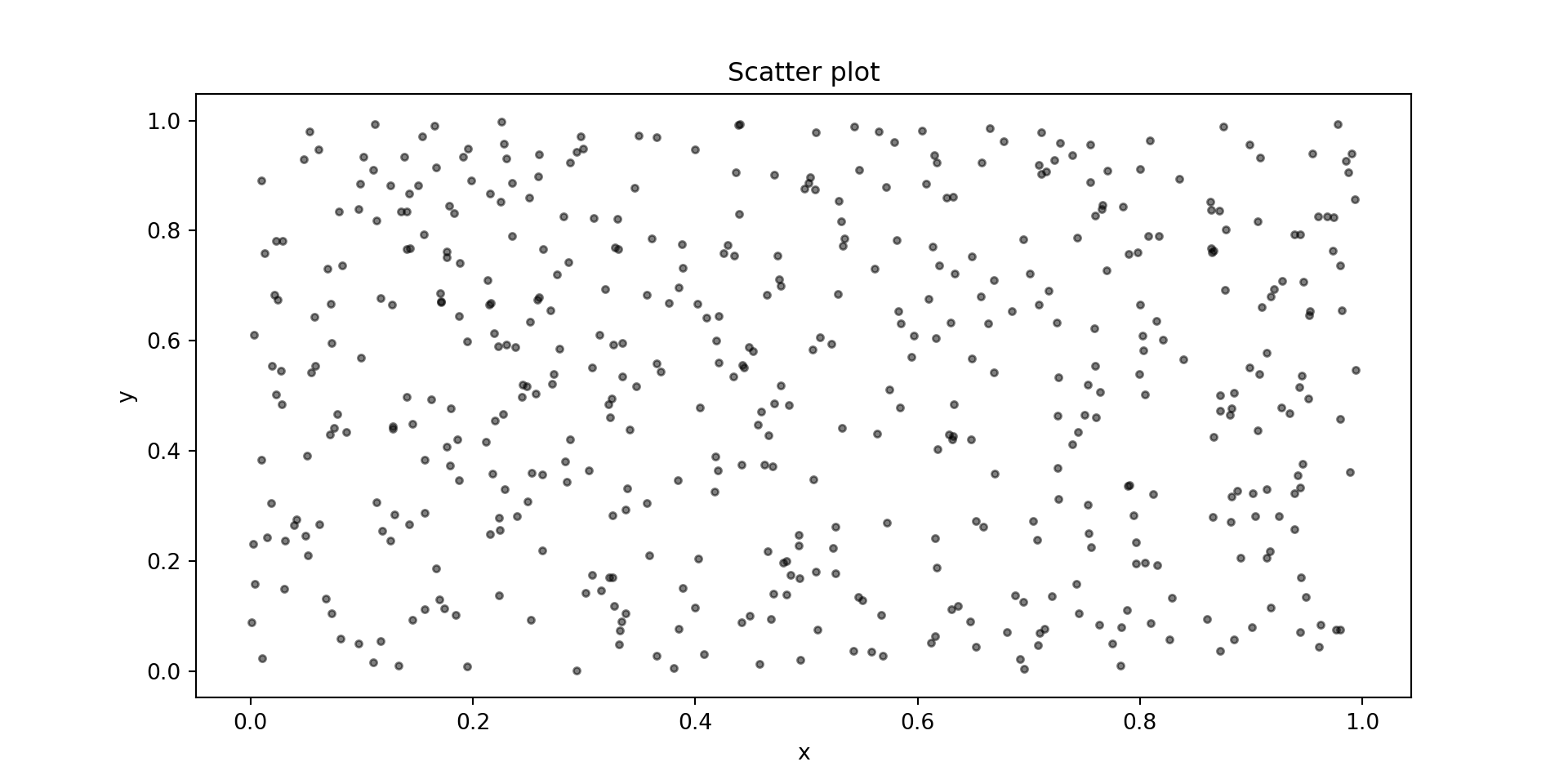
7 Dataframes en Python: `pandas`

Un dataframe es un “marco de datos”
Un dataframe es una estructura de dos dimensiones que pueden ser modificadas.
Los datos que contiene un dataframe pueden ser o no heterogéneos.
Los datos son alineados en una estructura de tabla en filas y columnas.
Los tres componentes principales de un dataframe son los datos, filas y columnas.

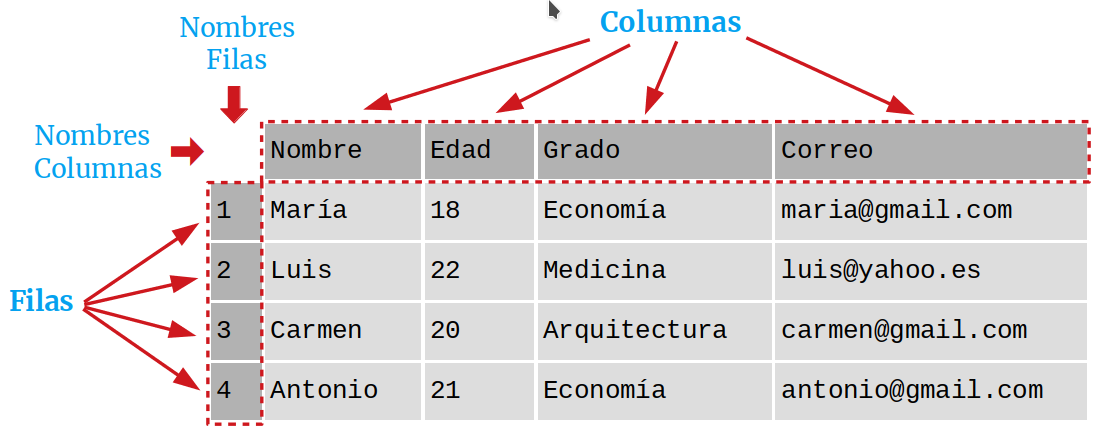
Ejemplo de Dataframe

Ahora emplearemos uno de los paquetes de Python asociado al trabajo con Dataframes, el paquete Pandas:

import pandas
pandas.DataFrame(data, index, columns, dtype, copy)

data: los datos pueden tomar varias formas, como arreglos de numpy, series, listas, diccionarios, etc.
index: para la etiqueta de las filas, Index es usada para la planilla resultante de datos. La opción por defecto toma np.arrange(n) si la indexación no es ingresada.
columns: Para las etiquetas de la columna, la sintaxis opcional por defecto es np.arrange(n). Esto es verdadero sólo si ninguna indexación es ingresada.
dtype: El tipo de dato para cada columna.
copy: este comando es usado para copiar los datos, si la opción por defecto es False.

Crear dataframe vacío

import pandas as pd
df = pd.DataFrame()
print(df)

Crear un dataframe desde una lista

#Ejemplo 1
import pandas as pd
data = [1,2,3,4,5]
df = pd.DataFrame(data)
print(df)

#Ejemplo 2
import pandas as pd
data = [['Alex',10],['Bob',12],['Clarke',13]]
df = pd.DataFrame(data,columns=['Name','Age'])
print (df)

#Ejemplo 3
import pandas as pd
data = [['Alex',10],['Bob',12],['Clarke',13]]
df = pd.DataFrame(data,columns=['Name','Age'],dtype=float)
print (df)

7.1 Creación de dataframes

Crear un dataframe desde un diccionario de ndarrays (arreglos)/listas

Todos los ndarrays deben ser del mismo largo. Si la indexación es ingresada, entonces el largo de los índices deben ser iguales al largo de los arreglos.
Si la indexación no es ingresada, entonces por defecto, la indexación será range(n), donde $n$ es el largo del arreglo.

#Ejemplo 1: Con indexación por defecto
import pandas as pd
data = {'Name':['Tom', 'Jack', 'Steve', 'Ricky'],'Age':[28,34,29,42]}
df = pd.DataFrame(data)
print (df)

#Ejemplo 2: con indexación establecida
import pandas as pd
data = {'Name':['Tom', 'Jack', 'Steve', 'Ricky'],'Age':[28,34,29,42]}
df = pd.DataFrame(data, index=['rank1','rank2','rank3','rank4'])
print (df)

Crear un dataframe desde una lista de diccionarios

Una lista de diccionarios puede ser ingresada como input para crear el dataframe. Las claves del diccionario son por defecto tomadas como nombres de las columnas.

#Ejemplo 1: Con una lista de diccionarios
import pandas as pd
data = [{'a': 1, 'b': 2},{'a': 5, 'b': 10, 'c': 20}]
df = pd.DataFrame(data)
print (df)

#Ejemplo 2: Con una lista de diccionarios, con indexación establecida
import pandas as pd
data = [{'a': 1, 'b': 2},{'a': 5, 'b': 10, 'c': 20}]
df = pd.DataFrame(data, index=['first', 'second'])
print (df)

#Ejemplo 3: Un ejemplo más completo con lista de diccionarios, 
#índices de fila y columna
import pandas as pd
data = [{'a': 1, 'b': 2},{'a': 5, 'b': 10, 'c': 20}]

#Con dos índices de columna, valores iguales a las claves del diccionario
df1 = pd.DataFrame(data, index=['first', 'second'], columns=['a', 'b'])

#Con dos índices de columna con un índice con otro nombre
df2 = pd.DataFrame(data, index=['first', 'second'], columns=['a', 'b1'])
print (df1)
print (df2)

Nota: El data frame df2 es creado con una columna de índices distinta que la clave del diccionario. Entonces, el rellenado de NaNs yace en su lugar. Mientras que df1 es creado con la columna índices igual a la de las claves del diccionario.