Deep Learning

DNN: Ejemplos y práctica

Autor/a

Afiliación

Francisco Plaza Vega

Ingeniería en Estadística

1 Ejemplo en R, librería `neuralnet`

Utilizaremos la librería neuralnet de R, y datos del repositorio del Center for Machine Learning and Intelligent Systems de la Universidad de California, en particular, el conjunto de datos Concrete Compressive Strength Data Sets.

2 Lectura de datos y preprocesamiento

Primero leemos los datos y creamos una función para normalizar los datos (escalamiento [0,1]). Los datos pueden ser encontrados en el material del curso.

library(readxl)
concrete_data<- read_excel("db/Concrete_Data.xls")
names(concrete_data)<-c("cement","slag","ash","water","superplastic",
                        "coarseagg","fineagg","age","strength")
normalize <- function(x) {
return((x - min(x)) / (max(x) - min(x)))
}

Los datos normalizados quedarán de la siguiente forma:

concrete_data_norm <- as.data.frame(lapply(concrete_data, normalize))
summary(concrete_data_norm$strength)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.0000  0.2663  0.4000  0.4172  0.5457  1.0000

summary(concrete_data$strength)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  2.332  23.707  34.443  35.818  46.136  82.599

Debido a que los datos ya están ordenamos aleatoriamente, simplemente dividimos en dos partes de 75 y 25 porciento, respectivamente

concrete_train <- concrete_data_norm[1:773, ]
concrete_test <- concrete_data_norm[774:1030, ]

3 Modelo 1

El modelo que emplearemos será una red simple de perceptrón multicapa (simple multilayer feedfoward network). A continuación cargamos la librería neuralnet y establecemos semilla y modelo.

library(neuralnet)
set.seed(411)
concrete_model <- neuralnet(strength ~ cement + slag + 
                            ash + water + superplastic 
                            + coarseagg + fineagg + age,
                            data = concrete_train)

plot(concrete_model, rep="best")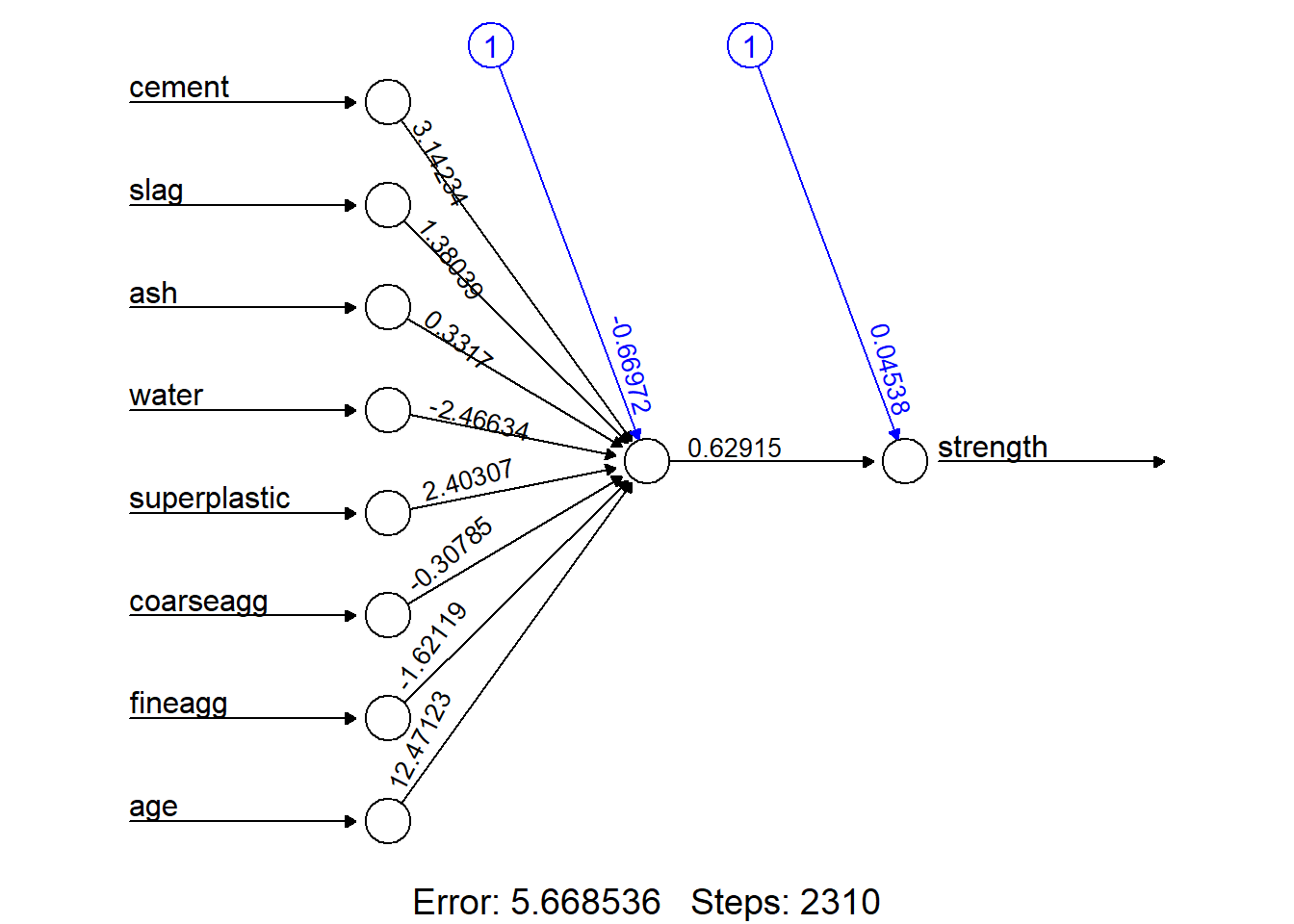

model_results <- compute(concrete_model, concrete_test[1:8])
predicted_strength <- model_results$net.result
cor(predicted_strength, concrete_test$strength)

          [,1]
[1,] 0.7209429

Debido a que es un problema de predicción, no podemos realizar una matriz de confusión para determinar el nivel de precisión

4 Modelo 2

concrete_model2 <- neuralnet(strength ~ cement + slag +
                               ash + water + superplastic +
                               coarseagg + fineagg + age,
                             data = concrete_train, hidden = 5)

plot(concrete_model2, rep="best")

model_results2 <- compute(concrete_model2, concrete_test[1:8])
predicted_strength2 <- model_results2$net.result
cor(predicted_strength2, concrete_test$strength)

          [,1]
[1,] 0.8138362

5 Modelo 3

En este problema no podemos utilizar una función de activación Rectified linear unit (ReLU) debido a que no tiene derivada en x=0. Alternativamente, utilizamos una función de activación llamada softplus o Smooth ReLI

softplus <- function(x) { log(1 + exp(x)) }
concrete_model3 <- neuralnet(strength ~ cement + slag +
                               ash + water + superplastic +
                               coarseagg + fineagg + age,
                             data = concrete_train,
                             hidden = c(5, 5), act.fct = softplus)

plot(concrete_model3, rep="best")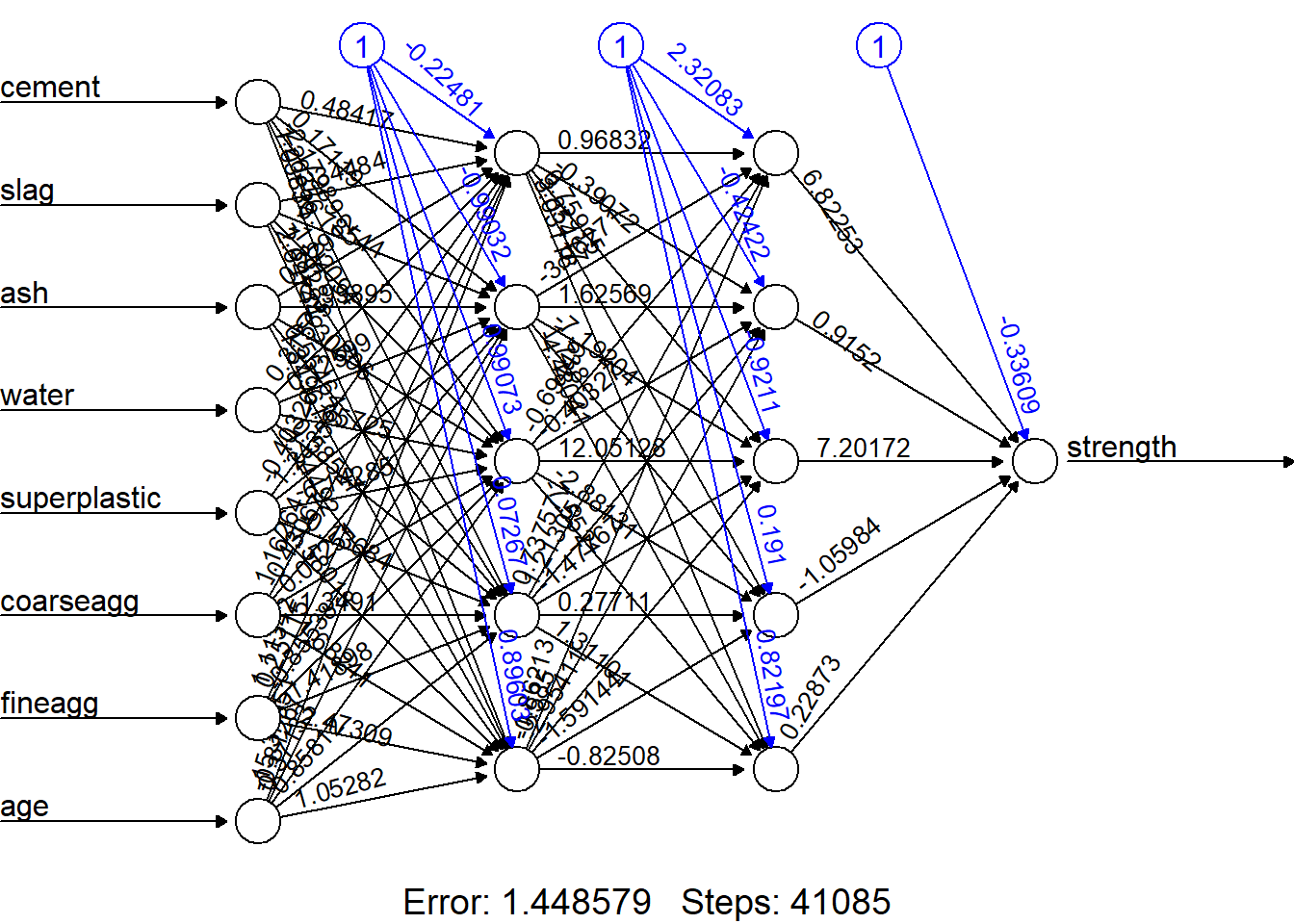

model_results3 <- compute(concrete_model3, concrete_test[1:8])
predicted_strength3 <- model_results3$net.result
cor(predicted_strength3, concrete_test$strength)

          [,1]
[1,] 0.6761314

strengths <- data.frame(actual = concrete_data$strength[774:1030],pred = predicted_strength3)
head(strengths, n = 3)

      actual      pred
774 37.42476 0.4099593
775 11.46599 0.2406689
776 22.43555 0.2818004

cor(strengths$pred, strengths$actual)

[1] 0.6761314

unnormalize <- function(x) {
return((x * (max(concrete_data$strength)) -
min(concrete_data$strength)) + min(concrete_data$strength))
}
strengths$pred_new <- unnormalize(strengths$pred)
strengths$error <- strengths$pred_new - strengths$actual
head(strengths, n = 3)

      actual      pred pred_new      error
774 37.42476 0.4099593 33.86232 -3.5624375
775 11.46599 0.2406689 19.87906  8.4130769
776 22.43555 0.2818004 23.27650  0.8409468

cor(strengths$pred_new, strengths$actual)

[1] 0.6761314

1 Ejemplo en R, librería neuralnet

2 Lectura de datos y preprocesamiento

3 Modelo 1

4 Modelo 2

5 Modelo 3

1 Ejemplo en R, librería `neuralnet`