Deep Learning

Unidad 4: Redes Neuronales Recurrentes (RNNs)

Francisco Plaza Vega

francisco.plaza.v@usach.cl

Ingeniería en Estadística

1 Redes Neuronales Recurrentes

1.1 Qué dice YouTube?

Algunos enlaces que pueden ser de interés

• Lecture 10: Recurrent Neural Networks -Stanford University School of Engineering
• MIT 6.S191(2021): Recurrent Neural Networks - Alexander Amini
• Illustrated Guide to LSTM’s and GRU’s: A step by step explanation - The AI Hacker
• Recurrent Neural Networks (RNNs), Clearly Explained!! - John Starmer

1.2 Datos secuenciales?

Datos secuenciales

Conjunto de observaciones recopiladas y ordenadas en función de un criterio temporal, espacial, o de cualquier otra dimensión en la que el orden de las observaciones sea esencial para su análisis.

• Los algoritmos típicos de aprendizaje supervisado asumen que la entrada es independiente e idénticamente distribuida (IID), lo que significa que los ejemplos de entrenamiento son mutuamente independientes y tienen la misma distribución subyacente.

• Si se tiene una muestra que consiste en \(n\) ejemplos de entrenamiento, \(x^{(1)}, x^{(2)}, \dots, x^{(n)}\), el orden en que se usan los datos para entrenar el algoritmo de aprendizaje automático no importa.

Ejemplo, los datos de iris
En el conjunto de datos **Iris**, cada flor ha sido medida de manera independiente, y las mediciones de una flor no influyen en las mediciones de otra flor.

library(datasets)
library(tidyverse)
data(iris)
iris %>% 
  slice_sample(n=10)

   Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
1           6.9         3.1          5.1         2.3  virginica
2           4.6         3.6          1.0         0.2     setosa
3           7.0         3.2          4.7         1.4 versicolor
4           4.4         2.9          1.4         0.2     setosa
5           5.1         3.7          1.5         0.4     setosa
6           5.1         3.5          1.4         0.2     setosa
7           5.6         2.5          3.9         1.1 versicolor
8           4.9         3.6          1.4         0.1     setosa
9           4.9         3.0          1.4         0.2     setosa
10          4.9         3.1          1.5         0.2     setosa

Lo anterior no funciona cuando trabajamos con secuencias, donde por definición, el orden sí importa.

Ejemplo: Datos financieros

• Supongamos que tenemos una muestra de \(n\) ejemplos de entrenamiento, que representa el valor de mercado de cierta acción en un día particular.

• Si el objetivo es predecir el valor del mercado de esa acción para los próximos tres días, tendría sentido considerar los precios previos en un orden cronológico, como al emplear un modelo Autoregresivo (AR) de series de tiempo.

• Precio de Bitcoin
• Código

library(cryptoQuotes)
library(xts)
library(tidyverse)
BTC <- get_quote(
  ticker   = "BTCUSDT",
  source   = "binance",
  futures  = FALSE,
  interval = "1d",
  from     = Sys.Date() - 90
)
data.frame(date = index(BTC),
           BTC = BTC$close) %>% 
  mutate(date = as.POSIXct(date)) %>% 
  ggplot()+
  geom_line(aes(x=date, y=close), color="#00a499", linewidth=1.5) +
  ylab("Precio de BTC en (USD)") + xlab("Días") +
  theme_minimal()

1.3 Series de tiempo

Un recordatorio… o no?

• Una serie de tiempo corresponde a una colección de observaciones \(y_t\), registradas en un tiempo específico \(t\).

• Usualmente \(t \in \mathbb{Z}\), donde \(\mathbb{Z} = \{..., -2, -1, 0, 1, 2, ... \}\) es un conjunto de valores enteros positivos y negativos. En la práctica, sólo una parte finita de los datos está disponible, donde podemos escribir la serie de tiempo como \(\{y_1, y_2, ..., y_n \}\).

• Formalmente, una serie de tiempo \(\{y_t \}\) corresponde a una realización de un proceso estocástico que está compuesto de variables aleatorias observadas a lo largo del tiempo.

• Una serie de tiempo de tipo discreta, es aquella en la que la colección de tiempos \(T_0\) en la que se hacen las observaciones es un conjunto discreto.

• Una serie de tiempo de tipo contínua es obtenida cuando las observaciones son tomadas de manera contínua sobre un intervalo de tiempo, por ejemplo \(T_0 = [0,1]\).

Una de las características principales de las series de tiempo es el hecho que observaciones sucesivas no son usualmente independientes, por lo que el análisis debe tomar en cuenta el orden temporal de las observaciones.

• Algunos ejemplos
• Vino
• TSM
• Contínua 1 y 2

library(tidyverse)
library(ggplot2)
library(readr)

# Vino ----
# URL de los datos
url <- "https://raw.githubusercontent.com/rajansharm/Time-Series-Analysis/refs/heads/master/AusWineSales.csv"

# Leer los datos desde el enlace
wine_data <- read_csv(url)

# Convertir el campo 'YearMonth' a formato de fecha
wine_data$YearMonth <- as.Date(paste0(wine_data$YearMonth, "-01"))

# Crear el gráfico
wine =
ggplot(wine_data, aes(x = YearMonth, y = Red)) +
  geom_line(color = "#00a499", linewidth = 0.7) +            
  geom_point(color = "#00a499", size = 2) +
  labs(
    x = "Años",
    y = "Ventas de vino tinto\n en Australia"
  ) +
  theme_bw()

library(tidyverse)
library(ggplot2)
library(readr)
library(zoo)

# SST ----
url <- "https://psl.noaa.gov/data/correlation/nina34.anom.data"
data_raw <- read_lines(url)
data_lines <- data_raw %>%
  .[-1] %>%                                # Eliminar automáticamente la primera línea
  .[str_detect(., "^[ ]*[0-9]{4}")]        # Mantener líneas que comienzan con un año de 4 dígitos

# Convertir las líneas en un data frame procesable
data <- data_lines %>%
  str_trim() %>%
  str_split("\\s+", simplify = TRUE) %>%
  as.data.frame(stringsAsFactors = FALSE) %>%
  set_names(c("Year", paste0("Month_", 1:12))) %>%
  mutate(across(everything(), as.numeric)) %>%
  pivot_longer(cols = starts_with("Month_"), names_to = "Month", values_to = "Temperature") %>%
  mutate(Month = as.numeric(str_remove(Month, "Month_")),
         Time = Year + (Month - 1) / 12) %>%
  filter(Temperature > -99)

# Calcular la media móvil de 5 años
data <- data %>%
  arrange(Time) %>%
  mutate(Moving_Avg = rollmean(Temperature, k = 60, fill = NA, align = "center")) # 5 años * 12 meses = 60

# Crear la gráfica
sst =  ggplot(data, aes(x = Time)) +
  geom_line(aes(y = Temperature), color = "#00a499", alpha = 1, size = 0.8) +
  geom_line(aes(y = Moving_Avg), color = "#ea7600", size = 1) + # Línea de tendencia
  labs(
    x = "Años",
    y = "TSM en la región\n Niño34 (°C)"
  ) +
  theme_bw()

library(tidyverse)
library(ggplot2)
library(latex2exp)

# Contínua 1 ----
cont1 = data.frame(t = seq(0,200)) %>% 
  mutate(N = rnorm(length(t)),
         x = cos(t/10) + N) %>% 
  ggplot(aes(x = t, y=x)) +
  geom_line(color = "#00a499", linewidth = 0.7) +            
  geom_point(color = "#00a499", size = 2) +
  xlab(TeX("t")) + 
  ylab(TeX("$X_t = cos(\\frac{t}{10})+N_t")) +
  theme_bw()

# Contínua 2 ----
cont2 = data.frame(t = seq(0,100)) %>% 
  mutate(x = cos(0.2*t + pi/3)) %>% 
  ggplot(aes(x = t, y=x)) +
  geom_line(color = "#00a499", linewidth = 0.7) +            
  geom_point(color = "#00a499", size = 2) +
  xlab(TeX("t")) + 
  ylab(TeX("$X_t = cos(0.2t + \\frac{\\pi}{3})")) +
  theme_bw()

1.4 Objetivos del análisis de series de tiempo

Existen distintos objetivos posibles del análisis de series de tiempo. Estos objetivos pueden ser clasificados en 4 categorías:

• Describir
• Explicar
• Predecir
• Controlar

1.5 Representando secuencias

A partir de las definiciones de Raschka y Mirjalili (2019)

1.6 Categorías en la modelación de secuencias

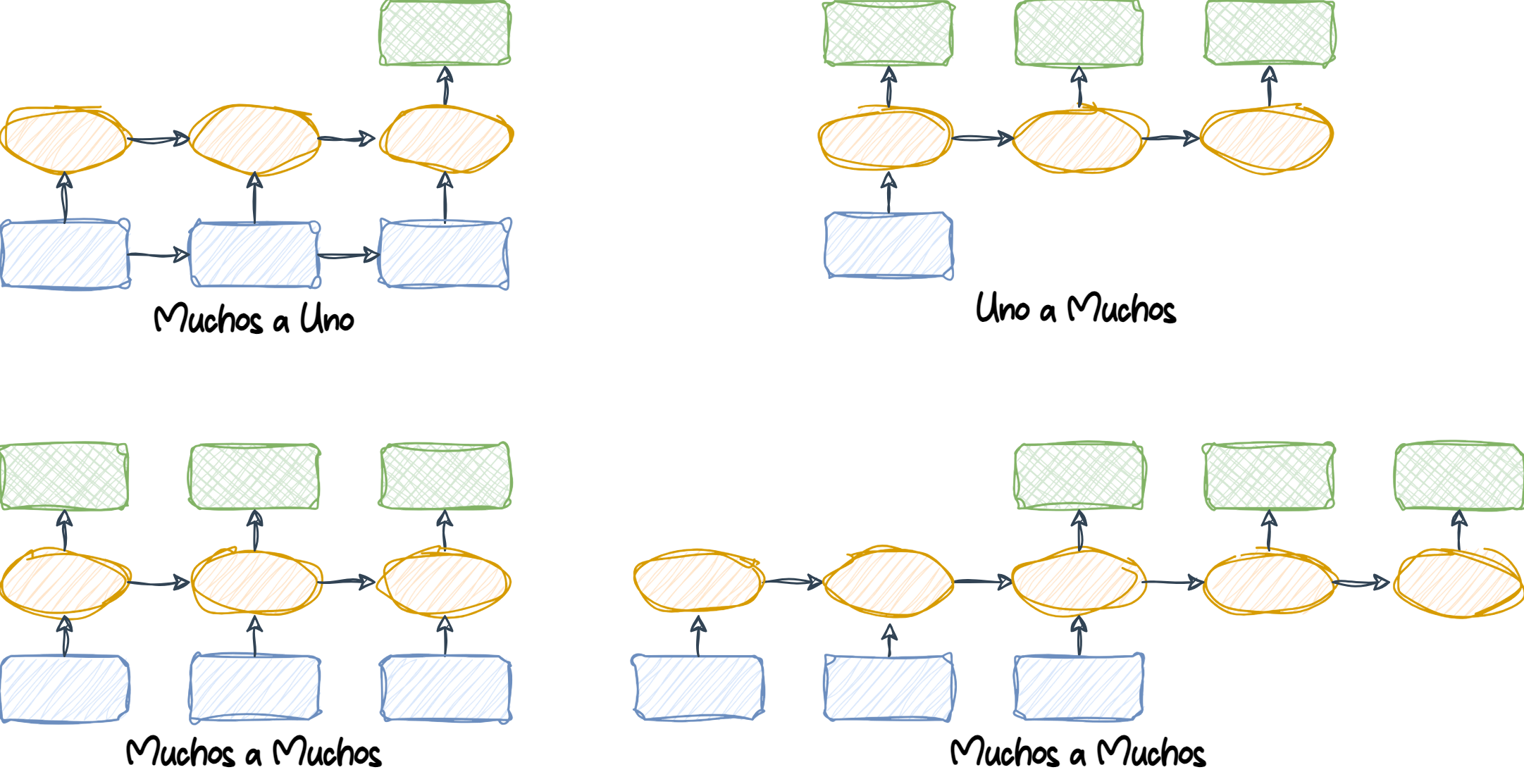
1.6.1 Muchos a uno

Many-to-one (Muchos a uno): Los datos de entrada son una secuencia, pero la salida es un vector o escalar de tamaño fijo, no una secuencia. Por ejemplo, en el análisis de sentimiento, la entrada es un texto (como una reseña de película) y la salida es una etiqueta de clase (por ejemplo, una etiqueta que indica si al crítico le gustó la película).

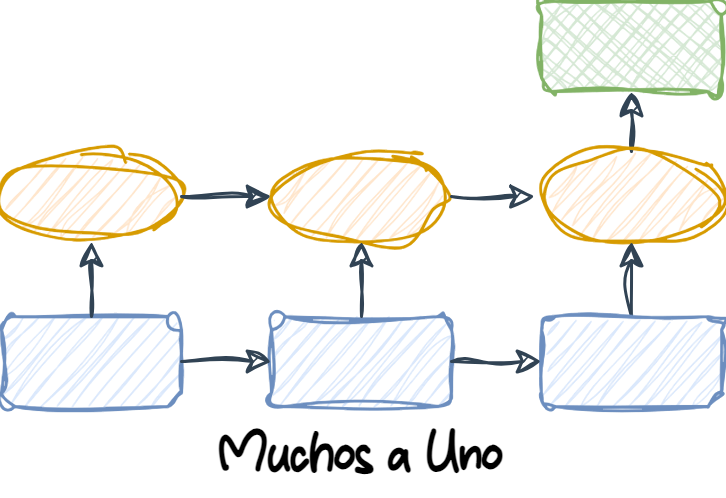
1.6.2 Uno a Muchos

One-to-many (Uno a muchos): Los datos de entrada están en formato estándar y no son una secuencia, pero la salida es una secuencia. Un ejemplo de esta categoría es la generación de subtítulos para imágenes: la entrada es una imagen y la salida es una frase en inglés que resume el contenido de esa imagen.

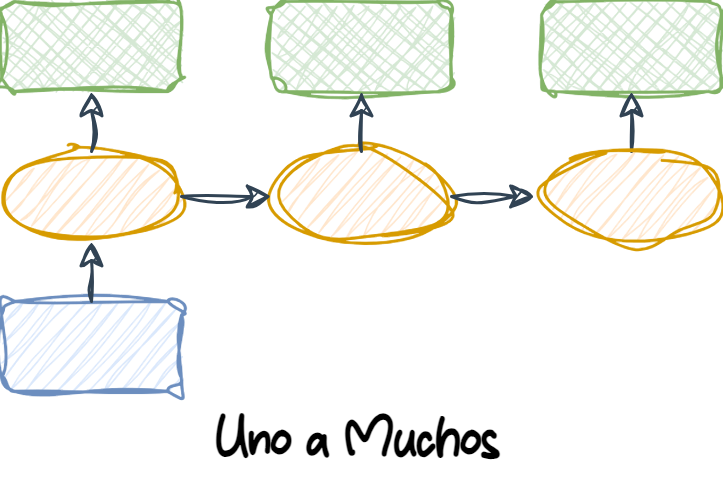
1.6.3 Muchos a Muchos

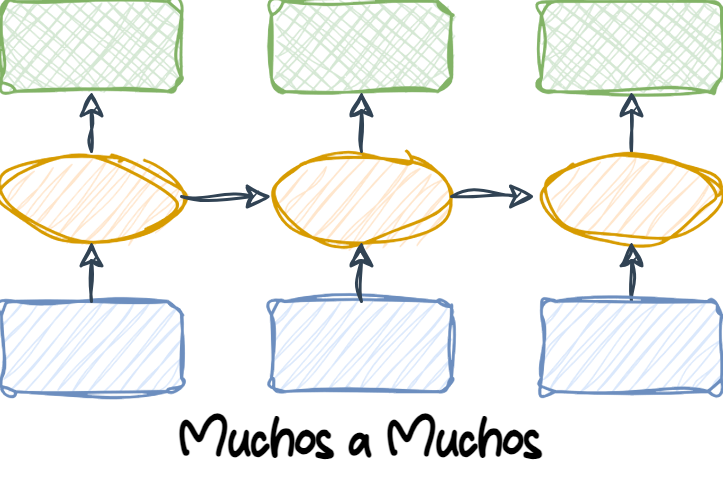
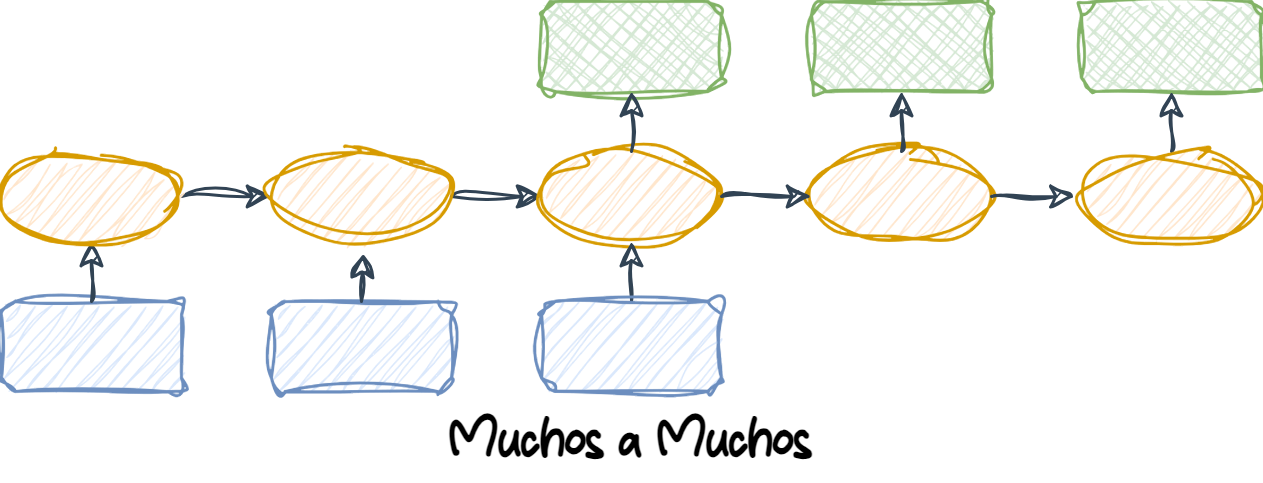
Many-to-many (Muchos a muchos): Tanto las entradas como las salidas son secuencias. Esta categoría puede dividirse aún más dependiendo de si las entradas y salidas están sincronizadas o no.

• Un ejemplo de una tarea many-to-many sincronizada es la clasificación de video, donde cada cuadro en un video está etiquetado.

• Un ejemplo de una tarea many-to-many con retraso sería la traducción de un idioma a otro. Por ejemplo, una frase completa en inglés debe ser procesada por una máquina antes de que se produzca su traducción al español.

2 RNN para secuencias

2.1 Entendiendo el mecanismo cíclico de las RNNs

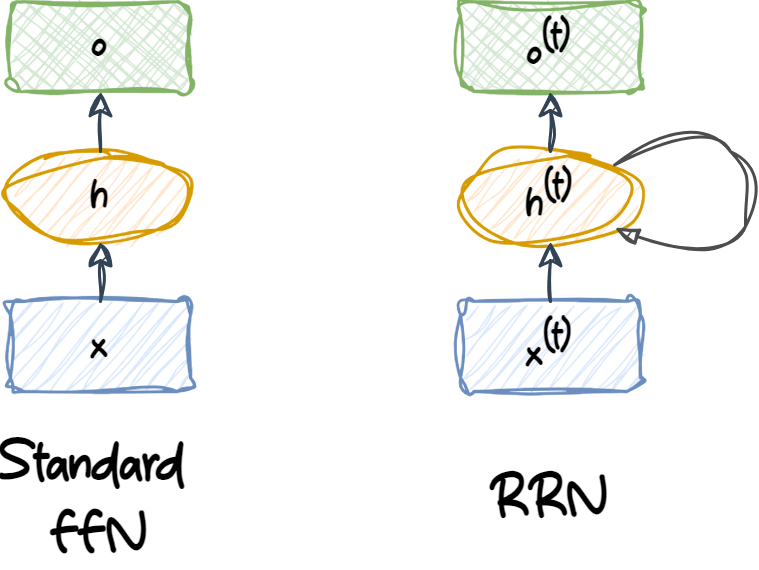
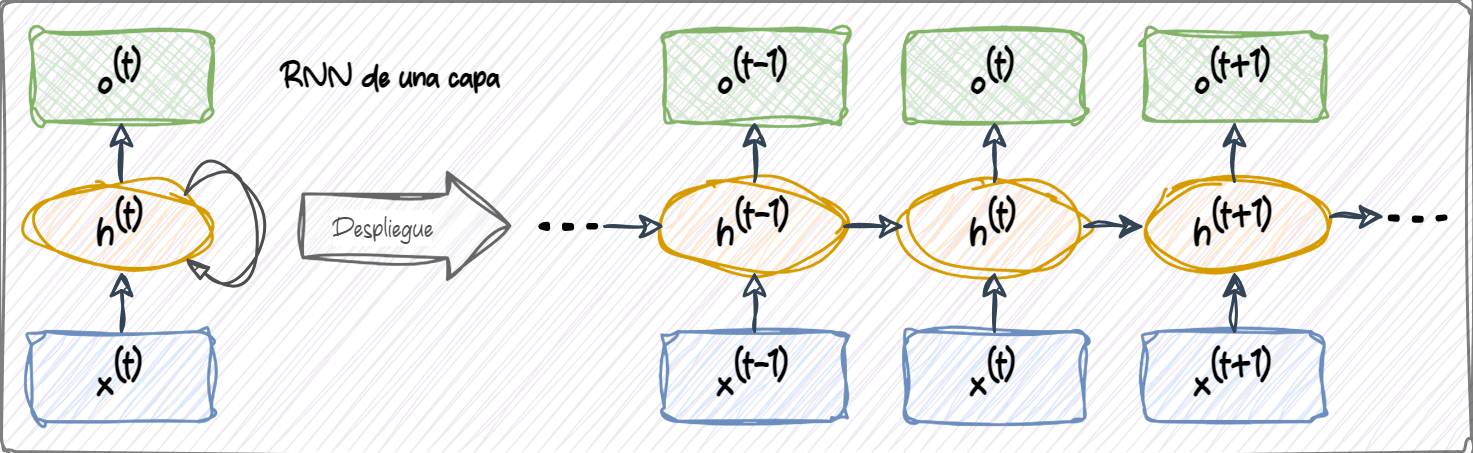
Ambas redes tienen solo una capa oculta. En esta representación, las unidades no se muestran, pero asumimos que la capa de entrada \((x)\), la capa oculta \((h)\) y la capa de salida \((o)\) son vectores que contienen muchas unidades.

• En una red feedforward estándar, la información fluye desde la capa de entrada hasta la capa oculta, y luego desde la capa oculta hasta la capa de salida. Por otro lado, en una RNN (Red Neuronal Recurrente), la capa oculta recibe su entrada tanto de la capa de entrada del instante de tiempo actual como de la capa oculta del instante de tiempo anterior.

• El flujo de información entre pasos de tiempo adyacentes en la capa oculta permite que la red tenga una memoria de eventos pasados. Este flujo de información se representa usualmente como un bucle, también conocido como un borde recurrente (recurrent edge) en notación de grafos, lo cual explica el origen del nombre de esta arquitectura general de RNN.

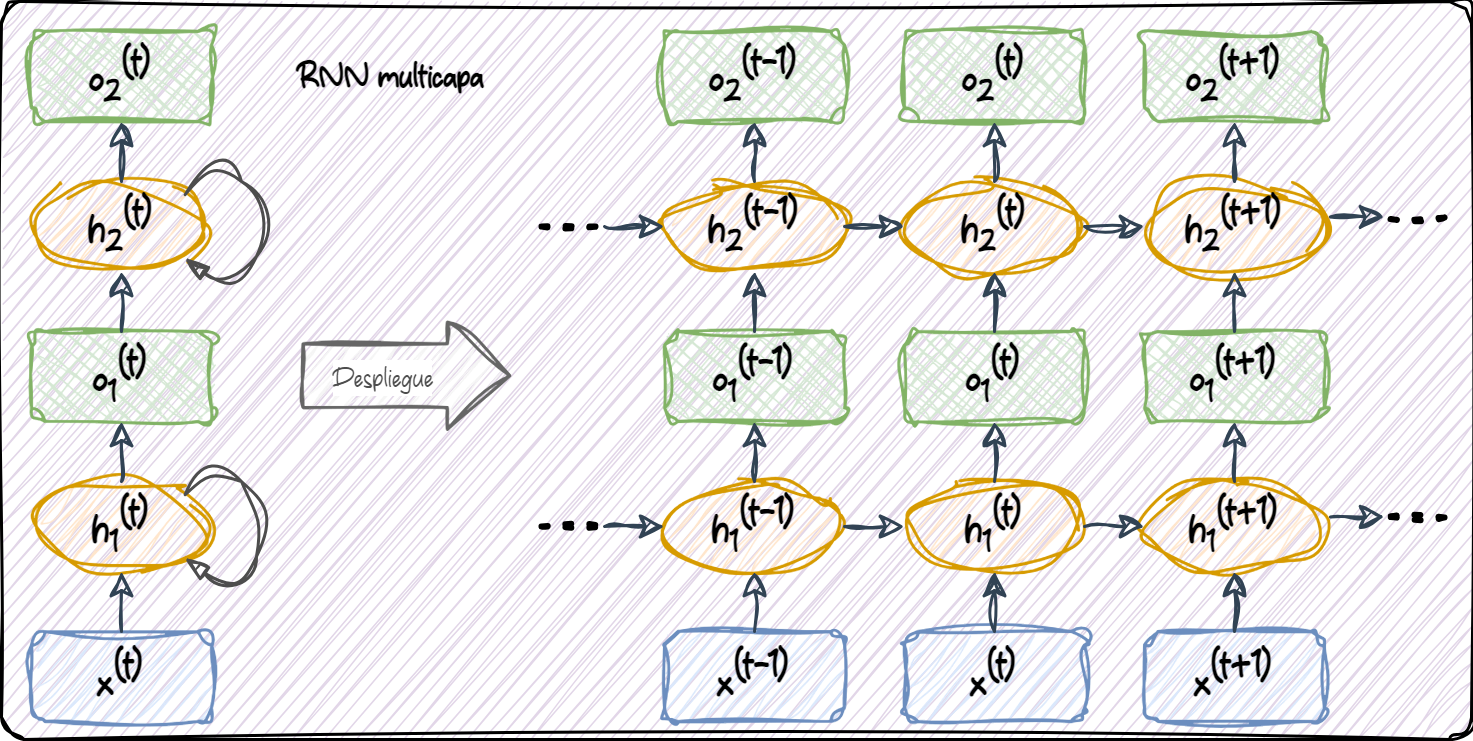
Similar a los MLP, las RNN pueden consistir en múltiples capas ocultas.

• Cada unidad oculta en una red neuronal estándar (MLP) recibe sólo una entrada: la preactivación neta asociada a la capa de entrada. Sin embargo, cada unidad oculta en una RNN recibe dos conjuntos distintos de entradas: la preactivación desde la capa de entrada y la activación de la misma capa oculta desde el paso de tiempo anterior, \(t - 1\).

• En el primer paso de tiempo, \(t = 0\), las unidades ocultas se inicializan en cero o con pequeños valores aleatorios. Luego, en un paso de tiempo donde \(t > 0\), las unidades ocultas reciben su entrada desde el punto de datos en el tiempo actual, \(x^{(t)}\), y desde los valores anteriores de las unidades ocultas en \(t - 1\), indicados como \(h^{(t-1)}\).

En el caso de una RNN multicapa:

• capa_1: La primera capa oculta se representa como \(\mathbf{h}_1^{(t)}\) y recibe su entrada desde el punto de datos \(\mathbf{x}^{(t)}\) y desde los valores ocultos de la misma capa, pero en el paso de tiempo anterior, \(\mathbf{h}_1^{(t-1)}\).

• capa_2: La segunda capa oculta, \(\mathbf{h}_2^{(t)}\), recibe sus entradas desde las salidas de la capa inferior en el paso de tiempo actual (\(\mathbf{o}_1^{(t)}\)) y desde sus propios valores ocultos del paso de tiempo anterior, \(\mathbf{h}_2^{(t-1)}\).

2.2 Cálculo de activaciones en una RNN

Para simplificar, consideraremos solo una capa oculta; sin embargo, el mismo concepto aplica a RNNs multicapa.

Cada borde dirigido (las conexiones entre cajas) en la representación de una RNN que acabamos de ver está asociado a una matriz de pesos. Estos pesos no dependen del tiempo \(t\), por lo tanto, se comparten a lo largo del eje temporal. Las distintas matrices de pesos en una RNN de una sola capa son las siguientes:

• \(\mathbf{W}_{xh}\): La matriz de pesos entre la entrada, \(\mathbf{x}^{(t)}\), y la capa oculta, \(\mathbf{h}\)

• \(\mathbf{W}_{hh}\): La matriz de pesos asociada al borde recurrente

• \(\mathbf{W}_{ho}\): La matriz de pesos entre la capa oculta y la capa de salida

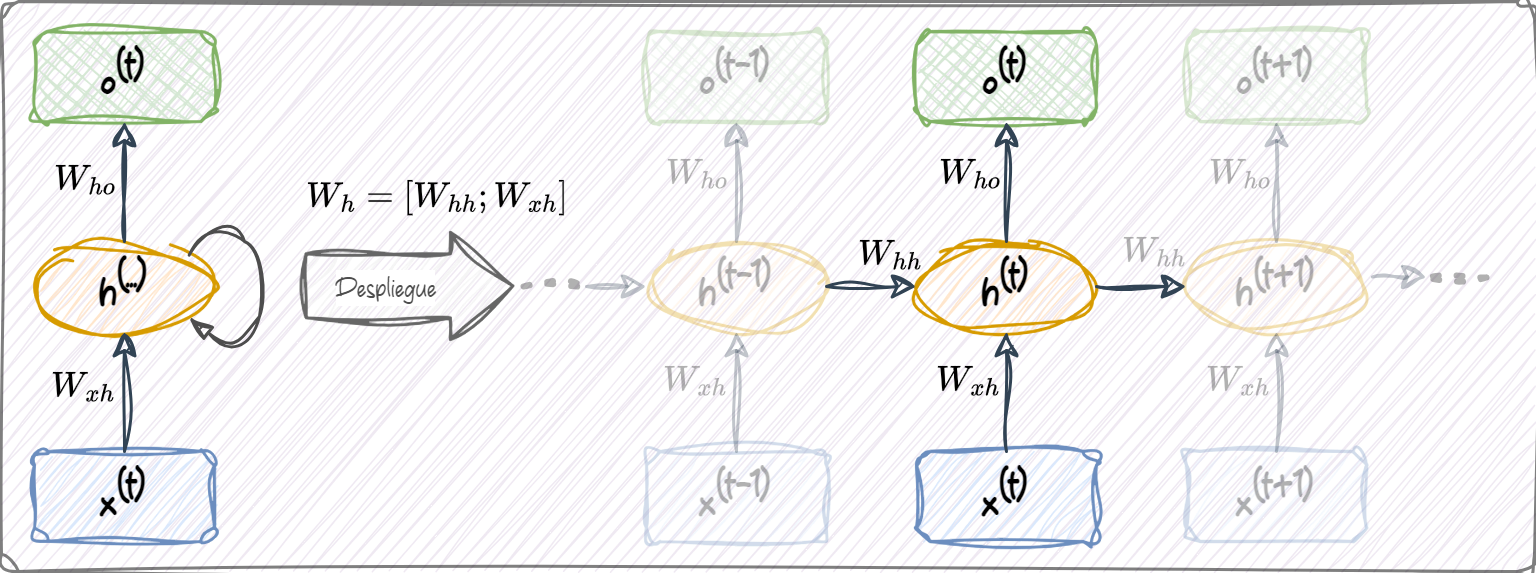
En ciertas implementaciones, puede observarse que las matrices de pesos, \(\mathbf{W}_{xh}\) y \(\mathbf{W}_{hh}\), se concatenan en una matriz combinada, \(\mathbf{W}_h = [\mathbf{W}_{xh} \, ; \, \mathbf{W}_{hh}]\). Más adelante en esta sección, también utilizaremos esta notación.

El cálculo de las activaciones es muy similar al de los perceptrones multicapa estándar y otros tipos de redes neuronales feedforward. Para la capa oculta, la entrada neta, \(\mathbf{z}_h\) (preactivación), se calcula mediante una combinación lineal, es decir, computamos la suma de las multiplicaciones de las matrices de pesos con los vectores correspondientes y añadimos el término de sesgo:

\[ \mathbf{z}_h^{(t)} = \mathbf{W}_{xh} \mathbf{x}^{(t)} + \mathbf{W}_{hh} \mathbf{h}^{(t-1)} + \mathbf{b}_h \]

Luego, las activaciones de las unidades ocultas en el instante de tiempo \(t\) se calculan de la siguiente manera:

\[ \mathbf{h}^{(t)} = \phi_h \left( \mathbf{z}_h^{(t)} \right) = \phi_h \left( \mathbf{W}_{xh} \mathbf{x}^{(t)} + \mathbf{W}_{hh} \mathbf{h}^{(t-1)} + \mathbf{b}_h \right) \]

Aquí, \(\mathbf{b}_h\) es el vector de sesgo para las unidades ocultas y \(\phi_h(\cdot)\) es la función de activación de la capa oculta.

En caso de que se desee utilizar la matriz de pesos concatenada, \(\mathbf{W}_h = [\mathbf{W}_{xh} \, ; \, \mathbf{W}_{hh}]\), la fórmula para calcular las unidades ocultas cambia de la siguiente manera:

\[ \mathbf{h}^{(t)} = \phi_h \left( \left[ \mathbf{W}_{xh} \, ; \, \mathbf{W}_{hh} \right] \begin{bmatrix} \mathbf{x}^{(t)} \\ \mathbf{h}^{(t-1)} \end{bmatrix} + \mathbf{b}_h \right) \]

Una vez que se han calculado las activaciones de las unidades ocultas en el paso de tiempo actual, se computan las activaciones de la capa de salida de la siguiente forma:

\[ \mathbf{o}^{(t)} = \phi_o \left( \mathbf{W}_{ho} \mathbf{h}^{(t)} + \mathbf{b}_o \right) \]

Para clarificar aún más este proceso, se muestra cómo se computan estas activaciones con ambas formulaciones.

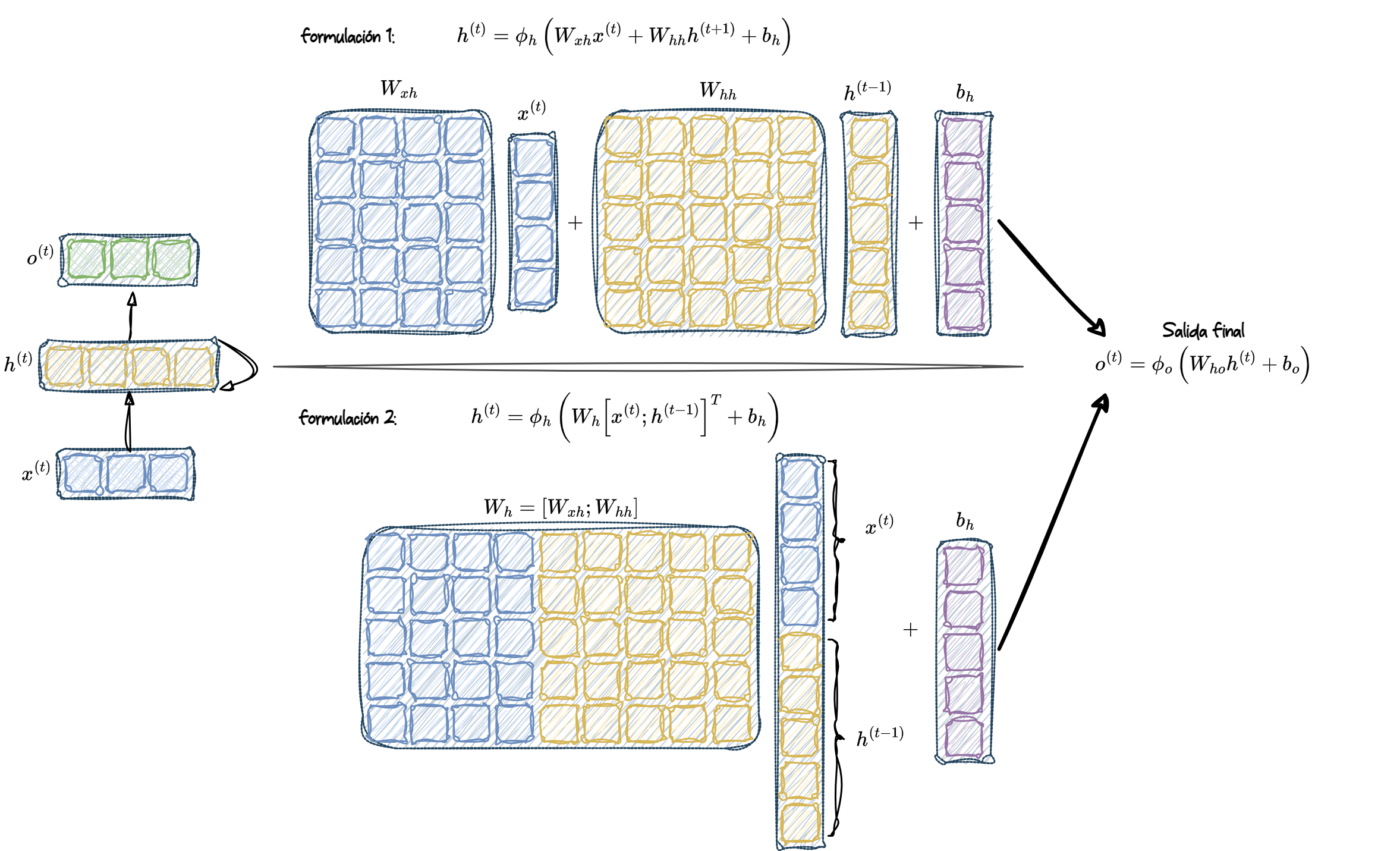
2.3 Entrenamiento de RNNs

El algoritmo de aprendizaje para RNNs fue introducido en 1990: Backpropagation Through Time: What It Does and How to Do It (Werbos 1990).

La derivación de los gradientes puede ser algo compleja, pero la idea básica es que la pérdida total, \(L\), es la suma de todas las funciones de pérdida en los tiempos \(t = 1\) hasta \(t = T\):

\[ L = \sum_{t=1}^{T} L^{(t)} \]

Dado que la pérdida en el tiempo \(t\) depende de las unidades ocultas en todos los pasos de tiempo anteriores \(1 : t\), el gradiente se calcula de la siguiente forma:

\[ \frac{\partial L^{(t)}}{\partial \mathbf{W}_{hh}} = \frac{\partial L^{(t)}}{\partial \mathbf{o}^{(t)}} \times \frac{\partial \mathbf{o}^{(t)}}{\partial \mathbf{h}^{(t)}} \times \left( \sum_{k=1}^{t} \frac{\partial \mathbf{h}^{(t)}}{\partial \mathbf{h}^{(k)}} \times \frac{\partial \mathbf{h}^{(k)}}{\partial \mathbf{W}_{hh}} \right) \]

Aquí, \(\frac{\partial \mathbf{h}^{(t)}}{\partial \mathbf{h}^{(k)}}\) se calcula como el producto de derivadas a través de los pasos de tiempo adyacentes:

\[ \frac{\partial \mathbf{h}^{(t)}}{\partial \mathbf{h}^{(k)}} = \prod_{i = k+1}^{t} \frac{\partial \mathbf{h}^{(i)}}{\partial \mathbf{h}^{(i-1)}} \]

Recurrencia en la capa oculta versus recurrencia en la capa de salida

Hasta ahora, hemos visto redes recurrentes en las que la capa oculta posee la propiedad recurrente. Sin embargo, es importante notar que existe un modelo alternativo en el cual la conexión recurrente proviene desde la capa de salida. En este caso, las activaciones netas de la capa de salida en el paso de tiempo anterior, \(\mathbf{o}^{t-1}\), pueden agregarse de una de las siguientes dos maneras:

• A la capa oculta en el paso de tiempo actual, \(\mathbf{h}^{t}\) (mostrado en la figura siguiente como output-to-hidden recurrence)

• A la capa de salida en el paso de tiempo actual, \(\mathbf{o}^{t}\) (mostrado en la figura siguiente como output-to-output recurrence)

3 Los desafíos de aprender interacciones de largo alcance

Back propagation through time (BPTT), introduce nuevos desafíos. Debido al factor multiplicativo, \(\frac{\partial \mathbf{h}^{(t)}}{\partial \mathbf{h}^{(k)}}\), en el cálculo de los gradientes de una función de pérdida, surgen los llamados problemas de gradientes que se desvanecen (vanishing) y gradientes que explotan (exploding).

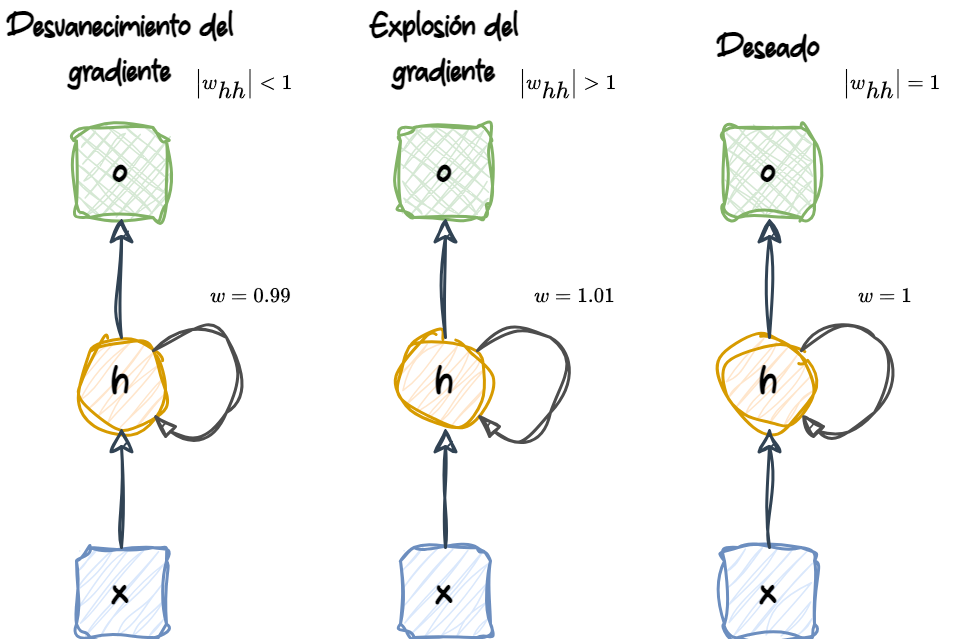
• Básicamente, \(\frac{\partial \mathbf{h}^{(t)}}{\partial \mathbf{h}^{(k)}}\) implica \(t - k\) multiplicaciones; por lo tanto, multiplicar el peso \(w\) por sí mismo \(t - k\) veces da como resultado un factor de \(w^{t-k}\):

  • Si \(|w| < 1\), este factor se vuelve muy pequeño cuando \(t - k\) es grande.

  • Por otro lado, si el peso del borde recurrente es \(|w| > 1\), entonces \(w^{t-k}\) se vuelve muy grande cuando \(t - k\) es grande.

• Cabe notar que un gran valor de \(t - k\) se refiere a dependencias de largo alcance (long-range dependencies). Podemos ver que una solución ingenua para evitar gradientes que se desvanecen o explotan es asegurar que \(|w| = 1\). Si estás interesado y deseas investigar esto en más detalle, puedes leer On the difficulty of training recurrent neural networks (Pascanu, Mikolov, y Bengio 2012).

En la práctica, existen al menos tres soluciones a este problema:

• Clipping de gradientes (Gradient clipping)

• Truncated Backpropagation Through Time (TBPTT)

• Long Short Term Memory Networks (LSTM)

• Al usar gradient clipping, se especifica un valor umbral o de corte para los gradientes, y se asigna este valor límite a los gradientes que lo exceden. En contraste, Truncated Backpropagation Through Time (TBPTT) limita la cantidad de pasos de tiempo hacia atrás que puede realizar la retropropagación después de cada paso hacia adelante. Por ejemplo, si la secuencia tiene 100 elementos o pasos, podríamos solo retropropagar los últimos 20 pasos de tiempo.

• Aunque tanto el gradient clipping como TBPTT pueden resolver el problema de los gradientes que explotan, la truncación limita el número de pasos en los que el gradiente puede fluir hacia atrás de manera efectiva y actualizar adecuadamente los pesos. Por otro lado, Long Short Term Memory (LSTM, Hochreiter y Schmidhuber (1997)), ha tenido más éxito al abordar los problemas de gradientes que se desvanecen y explotan, mientras modela dependencias de largo alcance mediante el uso de celdas de memoria (memory cells).

3.1 Esquema general de una celda LSTM

• Las LSTM fueron introducidas por primera vez para superar el problema de los gradientes que se desvanecen (vanishing gradient problem) en el artículo de Hochreiter y Schmidhuber (1997).

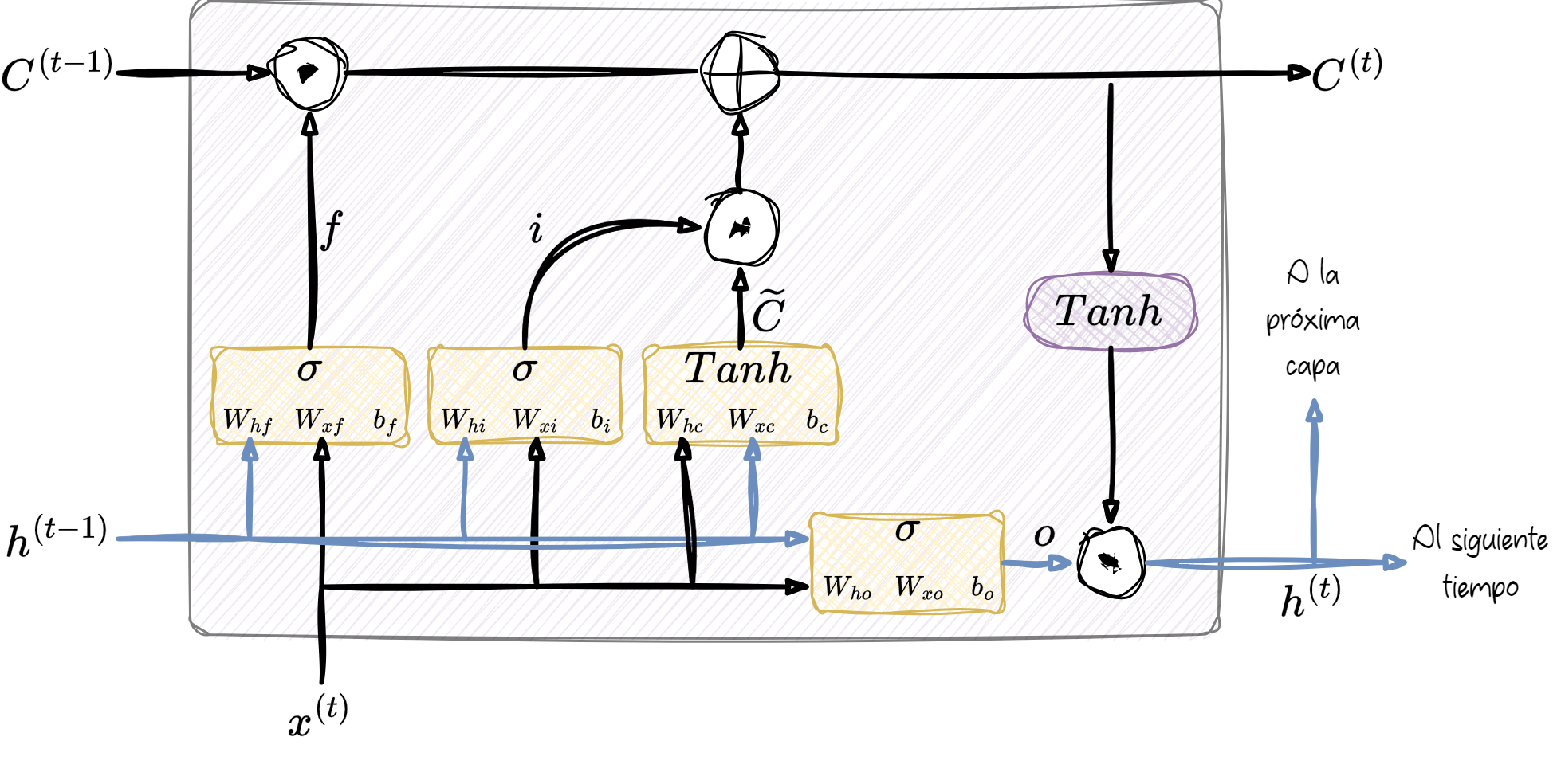
• El bloque fundamental de una LSTM es una celda de memoria (memory cell), que esencialmente representa o reemplaza la capa oculta de las RNN estándar.

La estructura interna de una celda LSTM muestran tres componentes fundamentales, conocidos como puertas (gates), que controlan el flujo de información dentro de la celda:

• Forget Gate (Puerta de olvido): decide qué parte de la información del estado de celda anterior \(\mathbf{c}^{(t-1)}\) debe ser descartada. Esta puerta evalúa qué tan relevante sigue siendo la información del pasado y produce una salida \(\mathbf{f}_t\) que modula dicha memoria.

• Input Gate (Puerta de entrada): regula qué nueva información, proveniente de la entrada actual \(\mathbf{x}^{(t)}\) y del estado oculto anterior \(\mathbf{h}^{(t-1)}\), será incorporada al estado de celda actual. La señal de esta puerta se denota como \(\mathbf{x}_t\) en el esquema.

• Output Gate (Puerta de salida): determina qué parte del estado de celda actualizado \(\mathbf{c}^{(t)}\) se convierte en la salida de la celda, es decir, en el nuevo estado oculto \(\mathbf{h}^{(t)}\) que se propaga al siguiente paso de tiempo o a la capa superior.

En cada celda de memoria, hay una conexión recurrente que tiene el peso deseable, \(w = 1\), como discutimos, para superar los problemas de gradientes que se desvanecen y explotan.
Los valores asociados con esta conexión recurrente se conocen colectivamente como estado de la celda (cell state).

Obsérvese que el estado de la celda del paso de tiempo anterior, \(\mathbf{c}^{(t-1)}\), se modifica para obtener el estado de la celda en el paso de tiempo actual, \(\mathbf{c}^{(t)}\), sin ser multiplicado directamente por ningún factor de peso.

El flujo de información en esta celda de memoria está controlado por varias unidades de cómputo (a menudo llamadas puertas o gates) que se describen aquí.
En la figura anterior: - \(\odot\) representa el producto elemento a elemento (element-wise product) - \(\oplus\) representa la suma elemento a elemento (element-wise addition)

Además: - \(\mathbf{x}^{(t)}\) se refiere a los datos de entrada en el tiempo \(t\) - \(\mathbf{h}^{(t-1)}\) indica las unidades ocultas en el tiempo \(t - 1\)

Cuatro recuadros están indicados con una función de activación, ya sea la función sigmoide (\(\sigma\)) o tangente hiperbólica (tanh), junto con un conjunto de pesos.
Estos recuadros aplican una combinación lineal realizando multiplicaciones de matrices y vectores sobre sus entradas (que son \(\mathbf{h}^{(t-1)}\) y \(\mathbf{x}^{(t)}\)).
Estas unidades de cómputo con funciones de activación sigmoide, cuyos valores de salida se pasan por \(\odot\), se denominan puertas (gates).

4 Referencias

Hochreiter, Sepp, y Jürgen Schmidhuber. 1997. «Long short-term memory». Neural computation 9 (8): 1735-80.

Pascanu, Razvan, Tomas Mikolov, y Yoshua Bengio. 2012. «On the difficulty of training Recurrent Neural Networks». arXiv e-prints, arXiv-1211.

Raschka, Sebastian, y Vahid Mirjalili. 2019. Python machine learning: Machine learning and deep learning with Python, scikit-learn, and TensorFlow 2. Packt Publishing Ltd.

Werbos, Paul J. 1990. «Backpropagation through time: what it does and how to do it». Proceedings of the IEEE 78 (10): 1550-60.