Simulación Estadística
Unidad 0: Preliminares
1 Probabilidades
Probabilidades
La noción básica de teoría de probabilidad nos indica que un experimento aleatorio es:
Un experimento cuyo resultado no puede ser determinado de manera adelantada.
Ejemplo:
Un ejemplo clásico es lanzar la moneda al aire. Supongamos que se lanza la moneda 3 veces. Entonces el espacio muestral, denotado por \(\Omega\), es el conjunto de todos los posibles resultados del experimento:
\[ \Omega = \{ C C C, C C S, C S C, C S S, S C C, S C S, S S C, S S S \} \] Los subconjuntos de \(\Omega\) son denominados eventos. Ejemplo: el evento \(A\) se define como que el tercer lanzamiento sea cara
\[ A = \{CCC, CSC, SCC, SSC \} \]
Decimos que el evento \(A\) ocurre si el resultado del experimento es alguno de los elementos en \(A\). Dado que los eventos son conjuntos, podemos aplicar las operaciones usuales a ellos, si definimos \(B\) como el que dos de tres lanzamientos sea cara
¿Cuál sería el resultado de?
- \(A \cup B\)
- \(A \cap B\)
- \(A^c\)
- \(B^c\)
Notar que si dos eventos \(A\) y \(B\) no tienen resultados en común, es decir \(A \cap B = \emptyset\), son denominados eventos disjuntos.
Conceptos básicos de probabilidad
- Espacio Muestral: Se define como el conjunto de todos los posibles resultados del experimento, lo anotamos por \(\Omega\)
- Suceso o Evento: Es cualquier subconjunto de \(\Omega\), usualmente lo anotamos con letras mayúsculas. \((A,B,C,\dots)\)
- Espacio de sucesos: Es el conjunto de todos los subconjuntos de \(\Omega\). Lo anotamos por \(2^{\Omega}\).
- Sigma Algebra: Es el conjunto de sucesos, \(\Gamma \subset 2^{\Omega}\), y que cumple con ciertas propiedades.
Clasificación del espacio muestral
- Discreto
- Numerable: Finito o Infinito.
- Continuo
- No numerable: Acotado o No acotado.
Definición formal de probabilidad
El par \((\Omega,\Gamma)\) se dice espacio medible, y la función \(\mathbb{P}:\Gamma \rightarrow \mathbb{R}^{+}\), es una medida de probabilidad si satisface:
\(0\leq \mathbb{P}[A] \leq 1, \forall A \in \Gamma\)
\(\mathbb{P}[\Omega]=1\)
Dados \(\displaystyle A_1,A_2,\dots \in \Gamma\), además \(A_1, A_2, \ldots, A_n\) disjuntos, entonces \(\displaystyle \mathbb{P}\left[ \bigcup_{i=1}^{n} A_n \right] = \sum_{i=1}^{n} \mathbb{P}[A_i], \hspace{5pt} \forall i\)
Este planteamiento probabilista, lleva a que los eventos del espacio muestral sean expresados de la forma más elemental posible, con el fin de poder aceptar la posibilidad de que cada posible resultado sea igualmente posible.
\[\mathbb{P}[A]=\dfrac{\#A}{\#\Omega}\]
Ejemplo:
Para el caso del ejemplo del lanzamiento de la moneda, la probabilidad de cualquier evento es dada de manera intuitiva, si la moneda es balanceada. Entonces
\[\mathbb{P}(\{CCC\}) = \cdots = \mathbb{P}(\{SSS\}) = 1/8\]
Dado que el evento \(A\) es la unión de las ocurrencias de \(\{CCC\}, \ldots \{ SSS\}\), la regla de la suma mostrada anteriormente puede ser aplicada. Con \(\#A\) representando el número de ocurrencias en \(A\) y \(\# \Omega = 8\).
Propiedades
\(\mathbb{P}[A]+\mathbb{P}[A^c]=\mathbb{P}[\Omega]\)
\(\mathbb{P}[\phi]=1-\mathbb{P}[\phi^c]=1-\mathbb{P}[\Omega]=0\)
\(\mathbb{P}[A \cup B]=\mathbb{P}[A]+\mathbb{P}[B] - \mathbb{P}[A\cap B]\) . Si este último término \((\mathbb{P}[A\cap B])\) es cero, se dice que \(A\) y \(B\) son eventos mutuamente excluyentes.
\(\mathbb{P}[A-B]=\mathbb{P}[A\cap B^c]\)
\(\mathbb{P}[A \cap B]=\mathbb{P}[A]\mathbb{P}[B]\). Si \(A\) y \(B\) son independientes.
2 Probabilidad Condicional e Independencia
Probabilidad Condicional
¿Cómo cambian las probabilidades cuando se conoce la ocurrencia de algún evento \(B \subset \Omega\)?
Dado que el resultado depende de \(B\), el evento \(A\) ocurrirá si y sólo si \(A \cap B\), y la probabilidad de ocurrencia puede escribirse como:
\[ \mathbb{P}(A | B)=\dfrac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)} \qquad(1)\]
Lo anterior, mide la probabilidad de que el evento \(B\) ocurra dado que el evento \(A\) ocurrió.
Ejemplo:
Retomando el ejemplo del lanzamiento de la moneda 3 veces. Sea \(B\) el evento de que el número total de caras sea dos. La probabilidad condicional del evento \(A\) que el primer lanzamiento sea cara, dada la ocurrencia de \(B\) es:
\[\frac{(2/8)}{(3/8)} = \frac{2}{3}\]
Re escribiendo la ecuación Ecuación 1 e intercambiando el rol de \(A\) y \(B\) tenemos
\[ \mathbb{P}(A \cap B) = \mathbb{P}(A) \mathbb{P}(B|A) \] Lo anterior puede ser generalizado como la regla multiplicativa de la probabilidad, que establece que para cualquier secuencia de eventos \(A_1, A_2, \ldots, A_n\)
\[ \mathbb{P}(A_1, \ldots, A_n) = \mathbb{P}(A_1) \mathbb{P}(A_2|A_1) \mathbb{P}(A_3 | A_1 A_2) \cdots \mathbb{P}(A_n|A_1 \cdots A_{n-1} ), \] usando la abreviatura \(A_1 A_2 \cdots A_k \equiv A_1 \cap A_2 \cap \cdots A_k.\)
Notar que si los eventos \(A\) y \(B\) son independientes se tiene:
\[\mathbb{P}[B|A]=\dfrac{\mathbb{P}[B]\mathbb{P}[A]}{\mathbb{P}[A]}=\mathbb{P}[B]\] Por lo que, en palabras, si los eventos son independientes, la probabilidad condicional se reduce a la probabilidad simple.
Independencia
Definición:
Los eventos \(A_1, A_2, \ldots\) son independientes si para cualquier \(k\) y cualquier elección de distintos índices \(i_i, i_2, \ldots, i_k\), \[
\mathbb{P}\left( A_{i_1} \cap A_{i_2} \cap \ldots \cap A_{i_k} \right) = \mathbb{P}(A_{i_2}) \cdots \mathbb{P}(A_{i_k})
\]
- Concepto crucial en estadística
- Da cuenta de la falta de información entre eventos. Se dice que eventos \(A\) y \(B\) son independientes si el saber sobre la ocurrencia de \(B\) no cambia la probabilidad de ocurrencia de \(A\).
- En muchos casos, la independencia de eventos es un supuesto del modelo. Esto es, se asume que existe una probabilidad \(\mathbb{P}\) tal que ciertos eventos son independientes.
Ejemplo
Lanzamos una moneda sesgada \(n\) veces. Sea \(p\) la probabilidad de obtener cara (para una moneda balanceada, \(p = 1/2\)). Denotemos por \(A_i\) al evento de que el \(i\)-ésimo lanzamiento resulte en cara, \(i = 1,\ldots, n\). Entonces, \(\mathbb{P}\) debe ser tal que los eventos \(A_1, \ldots, A_n\) sean independientes, y \(\mathbb{P}(A_i) = p\) para todo i. Estas dos reglas especifican completamente \(\mathbb{P}\). Por ejemplo, la probabilidad de que los primeros \(k\) lanzamientos sean cara y los últimos \(n - k\) sean sello es
\[\begin{align} \mathbb{P}(A_1 \cdots A_k A_{k+1}^c \cdots A_n^c) & =\mathbb{P}\left(A_1\right) \cdots \mathbb{P}\left(A_k\right) \mathbb{P}\left(A_{k+1}^{\mathfrak{c}}\right) \cdots \mathbb{P}\left(A_n^{\mathfrak{c}}\right) \\ & =p^k(1-p)^{n-k} \end{align}\]
Regla multiplicativa
Se refiere a la determinación de la probabilidad de ocurrencia conjunta de dos o más eventos. Para el caso de dos eventos, como se vio anteriormente, se tiene:
\[\mathbb{P}[A\cap B]=\mathbb{P}[A]\mathbb{P}[B|A]\]
En el caso de tres eventos, se tiene:
\[\mathbb{P}[A \cap B \cap C]=\mathbb{P}[A] \mathbb{P}[B|A] \mathbb{P}[C| (A \cap B)]\]
Ejemplo:
Sea \(A\) el evento en el cual un hombre vivirá 10 años más y sea \(B\) el evento en el cual su esposa viva 10 años más. Supongamos que \(\mathbb{P}(A)=\frac{1}{4}\) y \(\mathbb{P}(B)=\frac{1}{3}\). Supongamos que \(A\) y \(B\) son eventos independientes, encuentre la probabilidad de que en 10 años:
- Ambos estén vivos.
- Al menos uno esté vivo.
- Ninguno esté vivo.
- Solamente la esposa esté viva
Solución:
Sea \(A\) el evento en el cual un hombre vivirá 10 años más y sea \(B\) el evento en el cual su esposa viva 10 años más. Supongamos que \(\mathbb{P}(A)=\frac{1}{4}\) y \(\mathbb{P}(B)=\frac{1}{3}\). Supongamos que \(A\) y \(B\) son eventos independientes, encuentre la probabilidad de que en 10 años:
Ambos estén vivos: \(\mathbb{P}[A \cap B] = \mathbb{P}[A]\mathbb{P}[B] = \frac{1}{4}\frac{1}{3} = \frac{1}{12}\)
Al menos uno esté vivo: \(\mathbb{P}[A \cup B] = \mathbb{P}[A] + \mathbb{P}[B] -\mathbb{P}[A \cap B] = \frac{1}{4} + \frac{1}{3} -\frac{1}{12} = \frac{1}{2}\)
Ninguno esté vivo: \(\mathbb{P}[A^c \cap B^c] = \mathbb{P}[A^c]\mathbb{P}[B^c] = \frac{3}{4}\frac{2}{3} = \frac{1}{2}\)
Solamente la esposa esté viva: \(\mathbb{P}[A^c \cap B] = \mathbb{P}[A^c]\mathbb{P}[B] = \frac{3}{4}\frac{1}{3} = \frac{1}{4}\)
Ejemplo:
Considere que se tienen 10 sacos de semillas. Se sabe que 4 son de una variedad y el resto de otra. Un cliente compra 3 sacos. ¿Cuál es la probabilidad de que los sacos sean de las dos variedades?
\(A:{ \text{Los sacos comprados son de las dos variedades} }\)
\[\mathbb{P}[A]=\dfrac{\#A}{\#\Omega}=\dfrac{ C_{1}^{4} \times C_{2}^{6} +C_{2}^{4} \times C_{1}^{6} }{C_{3}^{10}}\]
3 Distribuciones de probabilidad y variables aleatorias
Distribuciones de probabilidad
La distribución de probabilidad acumulada (cdf, del inglés cumulative distribution function) de una variable aleatoria \(X\) es \(F_X\) y se define por
\[ F_X(x) = P(X\leq x), \qquad x \in \mathbb{R}. \]
La CDF tiene algunas propiedades:
- \(F_x\) es no-decreciente
- \(F_X\) es contínua hacia la derecha, esto es \(\underset{\epsilon \rightarrow 0^+}{lim} F_X(x+\epsilon) = F_X(x), \qquad \forall x \in \mathbb{R}\)
- \(\underset{x \rightarrow -\infty}{lim} F_X(x) = 0\) y \(\underset{x \rightarrow \infty}{lim} F_X(x) = 1\)
- Una variable aleatoria \(X\) es contínua si \(F_X\) es una función contínua.
- Una variable aleatoria \(X\) es discreta si \(F_X\) es una función escalonada
4 Variables aleatorias
Variables aleatorias
Una Variable aleatoria, es una función que permite trabajar cualquier espacio muestral de manera cuantitativa.
Definición:
Se dice que \(X\) es una variable aleatoria si es una función que toma los elementos de \(\Omega\) y los transforma en puntos sobre la recta de los reales. Esto es:
\[\begin{align*} X:\Omega \longrightarrow \mathbb{R}_x\\ \omega \longrightarrow X(\omega) \end{align*}\]
Tipos de variables aleatorias
Se dice que \(X\) es una Variable Aleatoria si es una función que toma valores en probabilidad, es decir, no se puede predecir con certeza sus resultados.
Una variable aleatoria es siempre cuantitativa y se puede clasificar en los siguientes grupos:
\[X(\omega) \begin{cases} \text{Discreto} \begin{cases} \text{Finito}\\ \text{Infinito} \end{cases}\\ \text{Continuo} \begin{cases} \text{Acotados}\\ \text{No Acotados} \end{cases} \end{cases}\]
Función de distribución
Si \(X\) es una variable aleatoria discreta, donde los valores que toma son: \(x_1,x_2,x_3,...,x_k,\) entonces se tiene que en \(\mathbb{R}\), se representan por:
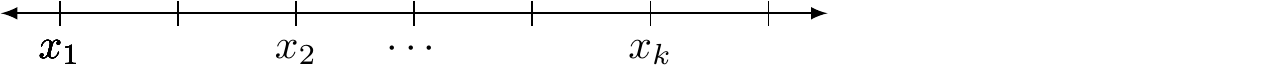
- Sobre la base de esta variable aleatoria discreta, cuyo concepto puede extender a variables continuas, se puede contruir la función de probabilidad acumulada, como la probabilidad de que la variable aleatoria \(X\) sea menor o igual a \(x \in \mathbb{R}\)
Definición
Sea \(X\) una variable aleatoria, se define la función de distribución de probabilidad, como la probabilidad de que la variable aleatoria \(X\) tome algún valor menor o igual que \(x \in \mathbb{R}\), y se simboliza por \(F_{X}(x)=P[X \leq x]\).
La función de distribución cumple con las siguientes propiedades:
- \(\displaystyle \lim_{x\rightarrow -\infty} F_{X}(x)= \lim_{x\rightarrow -\infty}P[X \leq x] = 0\)
- \(\displaystyle \lim_{x\rightarrow +\infty} F_{X}(x)= \lim_{x\rightarrow +\infty}P[X \leq x] = 1\)
En el caso que una variable sea cuantitativa, existe un continuo de valores que puede tomar \(x\), razón por la cual la función de distribución está dada por:
\[\displaystyle F_{X}(x)=P[X \leq x]=\int_{-\infty}^{x} f_{T}(t)dt\]

Función de densidad y distribución
Función de cuantía
Definición
Sea \(X\) una variable aleatoria discreta, entonces se define la función de cuantía o masa de probabilidad , como la probabilidad de que la variable aleatoria \(X\) tome un valor específico \(x\), se simboliza por \(f_X(x)=P[X=x]\).
La función de cuantía cumple con las siguientes propiedades
- \(f_X(x)=P[X=x] \geq 0 \hspace{10pt} \forall x \in \mathbb{R}\) - \(\displaystyle \sum_{x\in\mathbb{R}} P[X=x] =1\) - \(f_{X}(x)=P[X\leq x] - P[X \leq x-1]=F_{X}(x)-F_{X}(x-1)\)
Función de densidad
Sea \(X\) una variable aleatoria continua, entonces \(f_{X}(x)\) es una función de densidad de probabilidad para \(X\), si \(f_{X}(x)\) satisface las siguientes condiciones:
- \(f_{X}(x) \geq 0\) para casi todo \(x \in \mathbb{R}\)
- \(\displaystyle \int_{x\in \mathbb{R}} f_{X}(x)dx =1\)
En el caso de que una variable sea absolutamente continua, existe un continuo de valores que puede tomar \(x\), razón por la cual la función de densidad está dada por:
\[F_{X}(x)=P[X\leq x]=\int_{-\infty}^{x}f_T(t)dt \Leftrightarrow \dfrac{dF_{X}(x)}{dx}=f_{X}(x)\]
Valores esperados
Definición
Sea \(X\) una variable aleatoria, entonces se define el valor esperado de una función real \(g(X)\), como: \[
\begin{align*}
E[g(X)]=
\begin{cases}
\displaystyle \sum_{x\in \mathbb{R}} g(X)P[X=x]\\
\displaystyle \int_{x\in \mathbb{R}} g(X)f(x)dx
\end{cases}
\end{align*}
\]
Si \(g(X)=X\), diremos que el valor esperado o esperanza matemática de \(X\) es: \[ \begin{align*} E[X]= \begin{cases} \displaystyle \sum_{x\in \mathbb{R}} x P[X=x]\\ \displaystyle \int_{x\in \mathbb{R}} x f(x)dx \end{cases} \end{align*} \] Para variables de tipo discreta y continua, respectivamente.
Propiedades Valores Esperados
Sean \(a\) y \(b\) constantes, \(X\) una variable aleatoria entonces se cumple que:
- \(E[a]=a\)
- \(E[X]=\mu=\) constante
- \(E[aX]=aE[X]\)
- \(E[aX+b]=E[aX]+E[b]=aE[X]+b\)
Varianza
Sea \(X\) una variable aleatoria, se define el la de \(X\) como el valor esperado del cuadrado de la diferencia entre la variable aleatoria y su valor esperado, esto es: \[ \begin{align*} E[(X-E[X])^2]=V[X]= \begin{cases} \displaystyle\sum_{x\in\mathbb{R}} (X-E[X])^2P[X=x]\\ \displaystyle \int_{x\in\mathbb{R}} (X-E[X])^2f_{X}(x)dx \end{cases} \end{align*} \] Para variables de tipo discreta y continua, respectivamente.
Propiedades de la Varianza
Sea \(a\) y \(b\) constantes, \(X\) una variable aleatoria, entonces se cumple:
- \(V[a]=0\)
- \(V[X]=\sigma^2=\) constante
- \(V[aX]=a^2 V[X]\)
- \(V[aX+b]=V[aX]+V[b]=a^2V[X]+0=a^2V[X]\)
- \(V[X]=E[X^2]-(E[X])^2\)
5 Distribuciones de probabilidad
Algunas distribuciones contínuas
| Nombre | Notación | \(f(x)\) | \(x \in\) | Parametros |
|---|---|---|---|---|
| Uniforme | \(\mathrm{U}[\alpha, \beta]\) | \(\frac{1}{\beta-\alpha}\) | \([\alpha, \beta]\) | \(\alpha<\beta\) |
| Normal | \(\mathrm{N}\left(\mu, \sigma^2\right)\) | \(\frac{1}{\sigma \sqrt{2 \pi}} \mathrm{e}^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\) | \(\mathbb{R}\) | \(\sigma>0, \mu \in \mathbb{R}\) |
| Gamma | \(\mathrm{Gamma} (\alpha, \lambda)\) | \(\frac{\lambda^\alpha x^{\alpha-1} \mathrm{e}^{-\lambda x}}{\Gamma(\alpha)}\) | \(\mathbb{R}_{+}\) | \(\alpha, \lambda>0\) |
| Exponencial | \(\operatorname{Exp}(\lambda)\) | \(\lambda \mathrm{e}^{-\lambda x}\) | \(\mathbb{R}_{+}\) | \(\lambda>0\) |
| Beta | \(\operatorname{Beta}(\alpha, \beta)\) | \(\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}\) | \([0,1]\) | \(\alpha, \beta>0\) |
| Weibull | \(\mathrm{Weib}(\alpha, \lambda)\) | \(\alpha \lambda(\lambda x)^{\alpha-1} \mathrm{e}^{-(\lambda x)^\alpha}\) | \(\mathbb{R}_{+}\) | \(\alpha, \lambda>0\) |
| Pareto | \(\operatorname{Pareto}(\alpha, \lambda)\) | \(\alpha \lambda(1+\lambda x)^{-(\alpha+1)}\) | \(\mathbb{R}_{+}\) | \(\alpha, \lambda>0\) |
Algunas distribuciones discretas
| Nombre | Notación | \(f(x)\) | \(x \in\) | Parametros |
|---|---|---|---|---|
| Bernoulli | \(\operatorname{Ber}(p)\) | \(p^x(1-p)^{1-x}\) | \(\{0,1\}\) | \(0 \leqslant p \leqslant 1\) |
| Binomial | \(\operatorname{Bin}(n, p)\) | \(\binom{n}{r} p^{x}(1-p)^{n-x}\) | \(\{0,1, \ldots, n\}\) | \(0 \leqslant p \leqslant 1\), \(n \in \mathbb{N}\) |
| Discreta Uniforme | \(\operatorname{DU}\{1, \ldots, n\}\) | \(\frac{1}{n}\) | \(\{1, \ldots, n\}\) | \(n \in\{1,2, \ldots\}\) |
| Geométrica | \(\mathrm{G}(p)\) | \(p(1-p)^{x-1}\) | \(\{1,2, \ldots\}\) | \(0 \leqslant p \leqslant 1\) |
| Poisson | \(\operatorname{Poi}(\lambda)\) | \(\mathrm{e}^{-\lambda} \frac{\lambda^x}{x !}\) | \(\mathbb{N}\) | \(\lambda>0\) |
6 Funciones de variables aleatorias
Transformaciones lineales
Sea \(x = (x_1, \ldots, x_n)^T\) un vector columna en \(\mathbb{R}^n\) y \(A\) una matrix \(m \times n\). El mapear \(x \rightarrow z\), con \(z=Ax\) es denominado transformación lineal. Consideremos además un vector aleatorio \(\mathbf{X}=(X_1, \ldots, X_n)^T\), y
\[ \mathbf{Z} = A\mathbf{X} \]
El resultante \(\mathbf{Z}\) es un vector aleatorio en \(\mathbb{R}^m\). Si conocemos la distribución conjunta de \(\mathbf{X}\), entonces podríamos obtener la distribución contínua de \(\mathbf{Z}\).
Teorema
Si \(X\) tiene un vector de valores esperados \(\mu_\mathbf{X}\) y matriz de covarianza \(\Sigma_\mathbf{X}\), entonces el vector de valores esperados y la matriz de covarianza de \(\mathbf{Z} = A\mathbf{X}\) están dados por
\[\mu_\mathbf{Z} = A \mu_\mathbf{X}\] y \[\Sigma_\mathbf{Z} = A \Sigma_\mathbf{X} A^T \]
